This commit is contained in:
@@ -1,40 +0,0 @@
|
||||
branches: master
|
||||
|
||||
pipeline:
|
||||
build:
|
||||
when:
|
||||
path: [".woodpecker/*", "notes/*", "notes/src/*"]
|
||||
image: docker.io/sainnhe/mdbook:latest
|
||||
commands:
|
||||
- mdbook build notes
|
||||
deploy:
|
||||
when:
|
||||
path: [".woodpecker/*", "notes/*", "notes/src/*"]
|
||||
image: docker.io/sainnhe/vercel:latest
|
||||
secrets:
|
||||
- VERCEL_TOKEN
|
||||
- VERCEL_PROJECT_ID
|
||||
- VERCEL_ORG_ID
|
||||
commands:
|
||||
- vercel notes/book --token $VERCEL_TOKEN --prod
|
||||
notify:
|
||||
when:
|
||||
status:
|
||||
- failure
|
||||
image: docker.io/sainnhe/mailer:latest
|
||||
commands:
|
||||
- mailer
|
||||
secrets:
|
||||
[
|
||||
MAILER_FROM_ADDRESS,
|
||||
MAILER_FROM_NAME,
|
||||
MAILER_RECIPIENTS,
|
||||
MAILER_USER_NAME,
|
||||
MAILER_PASSWORD,
|
||||
MAILER_HOST,
|
||||
MAILER_PORT,
|
||||
MAILER_USE_STARTTLS,
|
||||
]
|
||||
environment:
|
||||
- MAILER_SUBJECT=Run Failed
|
||||
- MAILER_BODY=${CI_BUILD_LINK}
|
||||
1
notes/.gitignore
vendored
1
notes/.gitignore
vendored
@@ -1 +0,0 @@
|
||||
book
|
||||
@@ -1,6 +0,0 @@
|
||||
[book]
|
||||
authors = ["Sainnhe Park"]
|
||||
language = "en"
|
||||
multilingual = false
|
||||
src = "src"
|
||||
title = "Notes"
|
||||
@@ -1,80 +0,0 @@
|
||||
# Summary
|
||||
|
||||
# 数组
|
||||
|
||||
- [总结](./array.md)
|
||||
- [二分查找](./bin_search.md)
|
||||
- [移除元素](./remove_elements.md)
|
||||
- [长度最小的子数组](./minimum_size_subarray_sum.md)
|
||||
- [三数相加](./three_sum.md)
|
||||
|
||||
# 链表
|
||||
|
||||
- [总结](./linked_list.md)
|
||||
- [环形链表](./linked_list_cycle.md)
|
||||
|
||||
# 哈希表
|
||||
|
||||
- [总结](./hash_table.md)
|
||||
- [四数相加 II](./four_sum_ii.md)
|
||||
|
||||
# 字符串
|
||||
|
||||
- [总结](./string.md)
|
||||
- [替换空格](./substitute_spaces.md)
|
||||
- [翻转字符串里的单词](./reverse_words_in_a_string.md)
|
||||
- [左旋转字符串](./reverse_left_words.md)
|
||||
- [KMP](./kmp.md)
|
||||
- [重复的子字符串](./repeated_substring_pattern.md)
|
||||
|
||||
# 栈与队列
|
||||
|
||||
- [总结](./stack_and_queue.md)
|
||||
- [用栈实现队列 && 用队列实现栈](./impl_stack_queue.md)
|
||||
|
||||
# 二叉树
|
||||
|
||||
- [理论基础](./btree_basic.md)
|
||||
- [遍历](./btree_iter.md)
|
||||
- [二叉搜索树](./bstree.md)
|
||||
|
||||
# 回溯
|
||||
|
||||
- [总结](./backtrack.md)
|
||||
- [组合问题](./combinations.md)
|
||||
- [切割问题](./split.md)
|
||||
- [子集问题](./subsets.md)
|
||||
- [排列问题](./permute.md)
|
||||
- [棋盘问题](./chess.md)
|
||||
|
||||
# 贪心算法
|
||||
|
||||
- [总结](./greedy.md)
|
||||
|
||||
# 动态规划
|
||||
|
||||
- [总结](./dynamic-programming.md)
|
||||
- [基础问题](./dynamic-programming-basic.md)
|
||||
- [背包问题](./knapsack.md)
|
||||
- [打家劫舍](./house-robber.md)
|
||||
- [股票问题](./stock.md)
|
||||
- [子序列问题](./subsequence.md)
|
||||
|
||||
# STL
|
||||
|
||||
- [总结](./stl.md)
|
||||
- [排序](./stl_sorting.md)
|
||||
- [哈希表](./stl_hash_table.md)
|
||||
- [字符串](./stl_string.md)
|
||||
- [向量](./stl_vector.md)
|
||||
- [优先级队列](./stack_and_queue.md)
|
||||
|
||||
# 经典代码
|
||||
|
||||
- [排序算法](./sorting.md)
|
||||
- [二分查找](./bin_search.md)
|
||||
- [KMP](./kmp.md)
|
||||
- [单调队列](./stack_and_queue.md)
|
||||
- [二叉树遍历](./btree_iter.md)
|
||||
- [合并两个有序链表](./merge_two_sorted_linked_lists.md)
|
||||
- [LRU](./lru_cache.md)
|
||||
@@ -1,9 +0,0 @@
|
||||
# 总结
|
||||
|
||||
搜索有序数组中的元素:二分法。
|
||||
|
||||
原地移除数组中的元素:双指针,快指针满足条件时覆盖到慢指针。
|
||||
|
||||
当需要处理“连续子数组”时,考虑滑动窗口。
|
||||
|
||||
当使用双指针法时,考虑先排序,因为排序的时间复杂度是 O(n*logn) ,一般不会增加时间复杂度。
|
||||
@@ -1,62 +0,0 @@
|
||||
# 总结
|
||||
|
||||
使用场景:如果解决一个问题需要多个步骤,而每个步骤都在前一步的基础上进行选择,那么就可以用回溯法。
|
||||
|
||||
回溯法本质是在一棵树上进行深度优先遍历,因此需要设计好这棵树是如何生成的。
|
||||
|
||||
算法设计:
|
||||
|
||||
关键就是要学会分析和画图,然后确定传入参数。只要传入参数确定了代码框架就确定了 (返回值一般是 `void`):
|
||||
|
||||
- 思考这棵树怎么画,每层遍历的逻辑是什么,每条边的操作逻辑是什么。
|
||||
- 得设计一个数据结构 `NodeState` 来存放当前节点状态。该数据结构的可扩展性必须要强,需要满足以下条件:
|
||||
- 能描述当前节点的状态
|
||||
- 能作为最终结果存储
|
||||
- 能根据当前节点更新状态和撤销之前的更改
|
||||
- 得有一个 `&result` 来存放结果,这个 `&result` 通常是一个向量 `vector<NodeState> &`,里面存放了节点状态。
|
||||
- 其它传入参数用来完成每层遍历操作和每条边的操作。
|
||||
|
||||
设计完了数据结构之后来看看具体代码怎么写。模板如下:
|
||||
|
||||
```cpp
|
||||
void backtrack(NodeState &node, vector<NodeState> &result, int para1, int para2, int para3) {
|
||||
// 终止条件
|
||||
// 回溯法中的每个节点并不是真的树状节点,没有 `nullptr` ,因此用空指针来判断是否到了叶子结点并不合理,需要其它的一些方法来确定是否到达叶子节点,比如高度。
|
||||
if (/* end condition */) {
|
||||
/* update result */
|
||||
return;
|
||||
}
|
||||
|
||||
// 剪枝
|
||||
// 当现在的节点不可能出现我们想要的结果时,直接跳过。
|
||||
if (/* out of scope */) {
|
||||
return;
|
||||
}
|
||||
|
||||
// 遍历该节点的所有子节点,即遍历下一层
|
||||
for (...) {
|
||||
// 剪枝也可以在 for 循环中完成
|
||||
if (/* out of scope */) {
|
||||
continue;
|
||||
}
|
||||
// 处理节点
|
||||
// 现在 node 中的数据描述的是当前节点,
|
||||
// handle(node) 一般是让 node 中的数据变成子节点的数据
|
||||
handle(node);
|
||||
// 递归
|
||||
backtrack(node, result, para1, para2, para3);
|
||||
// 撤销数据处理,让 node 中的数据再次变回描述当前节点的数据
|
||||
revert(node);
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
回溯法的一个很重要的考点在于如何去重。去重有两种思路,一个是用哈希表记录每一层的使用情况,另一种是排序 + 判断,后者性能更好所以优先选择后者。
|
||||
|
||||
具体算法参考 [40. 组合总和 II](./combinations.html) 和 [491. 递增子序列](./subsets.html)
|
||||
|
||||
复杂度分析:
|
||||
|
||||
- 时间复杂度:最长路径长度 × 搜索树的节点数
|
||||
- 空间复杂度:一个节点所需要的空间 × 搜索树的节点数
|
||||
|
||||
@@ -1,64 +0,0 @@
|
||||
# 二分查找
|
||||
|
||||
适用于数组有序的情况下查找目标值。
|
||||
|
||||
## 写法一
|
||||
|
||||
针对左闭右闭区间(即 `[left, right]`):
|
||||
|
||||
```cpp
|
||||
class Solution {
|
||||
public:
|
||||
int search(vector<int>& nums, int target) {
|
||||
int left = 0;
|
||||
int right = nums.size() - 1; // 定义target在左闭右闭的区间里,[left, right]
|
||||
while (left <=
|
||||
right) { // 当left==right,区间[left, right]依然有效,所以用 <=
|
||||
int middle =
|
||||
left + ((right - left) / 2); // 防止溢出 等同于(left + right)/2
|
||||
if (nums[middle] > target) {
|
||||
right = middle - 1; // target 在左区间,所以[left, middle - 1]
|
||||
} else if (nums[middle] < target) {
|
||||
left = middle + 1; // target 在右区间,所以[middle + 1, right]
|
||||
} else { // nums[middle] == target
|
||||
return middle; // 数组中找到目标值,直接返回下标
|
||||
}
|
||||
}
|
||||
// 未找到目标值
|
||||
return -1;
|
||||
}
|
||||
};
|
||||
```
|
||||
|
||||
## 写法二
|
||||
|
||||
针对左闭右开(即 `[left, right)`):
|
||||
|
||||
```cpp
|
||||
class Solution {
|
||||
public:
|
||||
int search(vector<int>& nums, int target) {
|
||||
int left = 0;
|
||||
int right = nums.size(); // 定义target在左闭右开的区间里,即:[left, right)
|
||||
while (left < right) { // 因为left == right的时候,在[left,
|
||||
// right)是无效的空间,所以使用 <
|
||||
int middle = left + ((right - left) >> 1);
|
||||
if (nums[middle] > target) {
|
||||
right = middle; // target 在左区间,在[left, middle)中
|
||||
} else if (nums[middle] < target) {
|
||||
left = middle + 1; // target 在右区间,在[middle + 1, right)中
|
||||
} else { // nums[middle] == target
|
||||
return middle; // 数组中找到目标值,直接返回下标
|
||||
}
|
||||
}
|
||||
// 未找到目标值
|
||||
return -1;
|
||||
}
|
||||
};
|
||||
```
|
||||
|
||||
## 相关题目
|
||||
|
||||
- [704. 二分查找](https://leetcode.com/problems/binary-search/)
|
||||
- [35. 搜索插入位置](https://leetcode.com/problems/search-insert-position/)
|
||||
- [34. 在排序数组中查找元素的第一个和最后一个位置](https://leetcode.com/problems/find-first-and-last-position-of-element-in-sorted-array/)
|
||||
@@ -1,8 +0,0 @@
|
||||
# 二叉搜索树
|
||||
|
||||
- [s0235](https://leetcode.cn/problems/lowest-common-ancestor-of-a-binary-search-tree/description/): 找两个指定节点的最近公共祖先。思路很简单,只要出现分岔(即一个在当前节点的左边,一个在当前节点的右边),那么这个分岔点就是最近公共祖先。
|
||||
- [s0701](https://leetcode.cn/problems/insert-into-a-binary-search-tree/description/): 插入节点。一层一层往下找,直到发现找不到了就在这个地方插入。
|
||||
- [s0450](https://leetcode.cn/problems/delete-node-in-a-bst/description/): 删除节点。递归删除。
|
||||
- [s0669](https://leetcode.cn/problems/trim-a-binary-search-tree/description/): 修剪 BST 。递归修剪。
|
||||
- [s0108](https://leetcode.cn/problems/convert-sorted-array-to-binary-search-tree/): 有序数组转 BST 。数组中点为根节点,中点左侧部分生成左子树,右侧部分生成右子树,递归。
|
||||
- [s0538](https://leetcode.cn/problems/convert-bst-to-greater-tree/description/): BST 转累加树。可以找到每个节点的构建方法然后用直观一点的递归方式来写,不过本题有个特殊之处在于累加树的生成方式正好和反序中序遍历的遍历路径相同,因此可以用反序中序遍历来遍历生成。
|
||||
@@ -1,76 +0,0 @@
|
||||
# 理论基础
|
||||
|
||||
## 二叉树的种类
|
||||
|
||||
满二叉树:如果一棵二叉树只有度为 0 的结点和度为 2 的结点,并且度为 0 的结点在同一层上,则这棵二叉树为满二叉树。
|
||||
|
||||
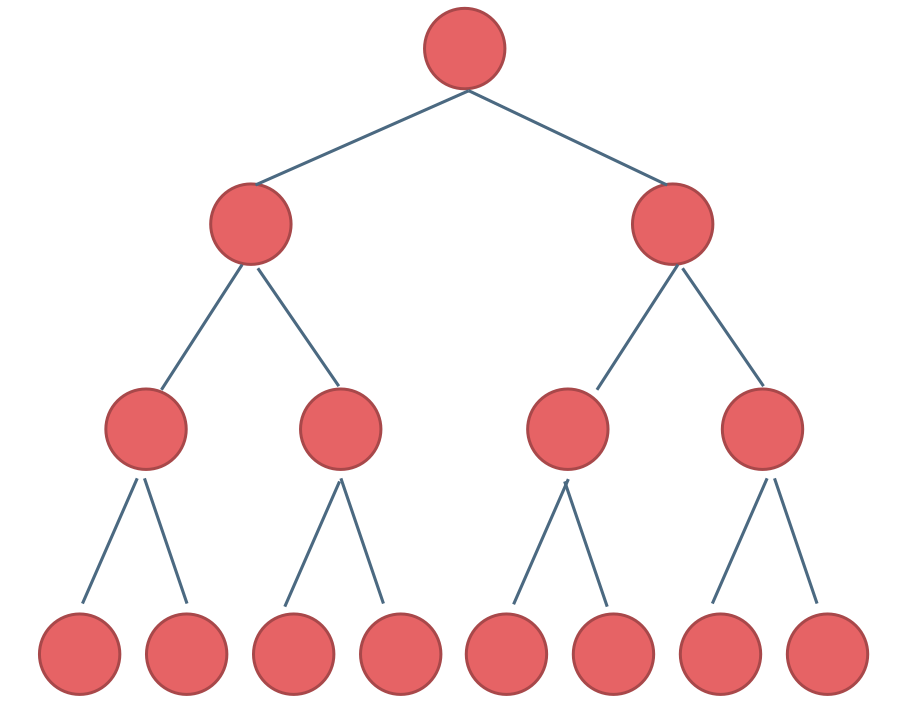
|
||||
|
||||
完全二叉树:除了最底层节点可能没填满外,其余每层节点数都达到最大值,并且最下面一层的节点都集中在该层最左边的若干位置。
|
||||
|
||||
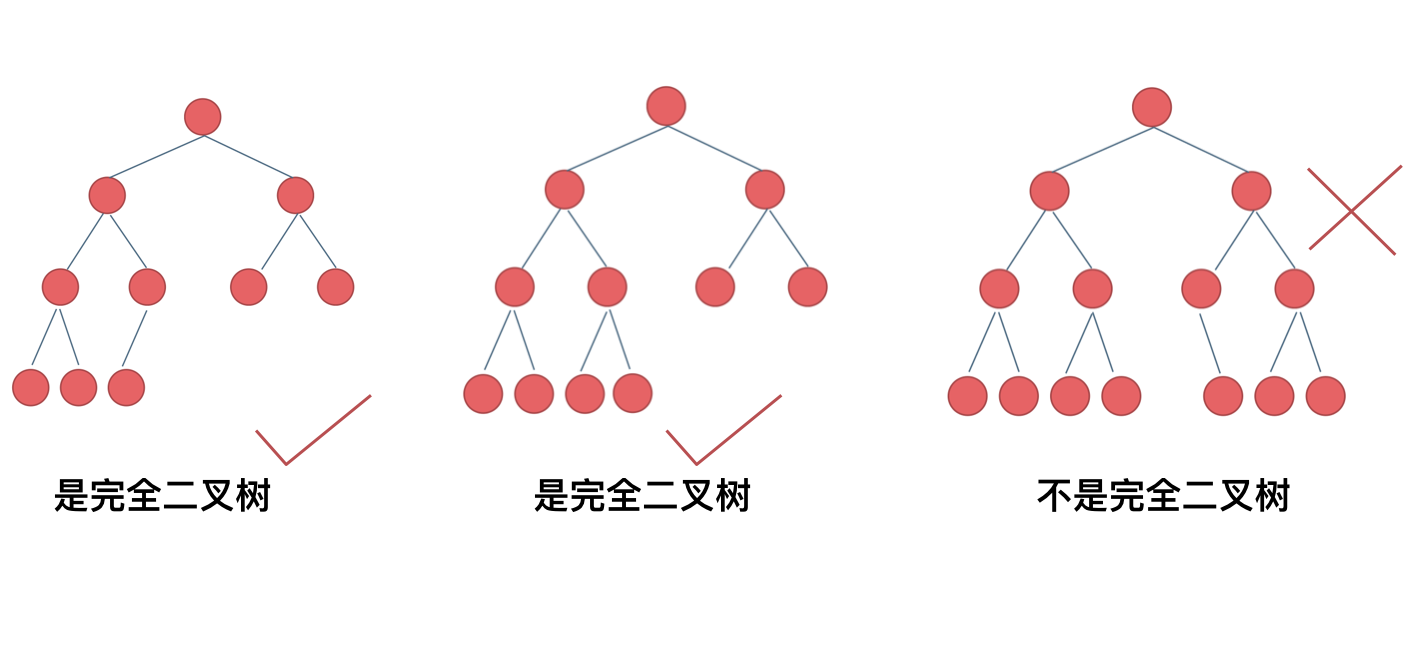
|
||||
|
||||
二叉搜索树:
|
||||
|
||||
- 若它的左子树不空,则左子树上所有结点的值均小于它的根结点的值;
|
||||
- 若它的右子树不空,则右子树上所有结点的值均大于它的根结点的值;
|
||||
- 它的左、右子树也分别为二叉排序树。
|
||||
|
||||
|
||||
|
||||
平衡二叉搜索树:又被称为 AVL(Adelson-Velsky and Landis)树,且具有以下性质:它是一棵空树或它的左右两个子树的高度差的绝对值不超过 1,并且左右两个子树都是一棵平衡二叉树。
|
||||
|
||||
|
||||
|
||||
## 二叉树的存储方式
|
||||
|
||||
1. 链式,用链表来存储
|
||||
|
||||
```cpp
|
||||
struct TreeNode {
|
||||
int val;
|
||||
TreeNode *left;
|
||||
TreeNode *right;
|
||||
TreeNode(int x) : val(x), left(NULL), right(NULL) {}
|
||||
};
|
||||
```
|
||||
|
||||
2. 数组存储
|
||||
|
||||
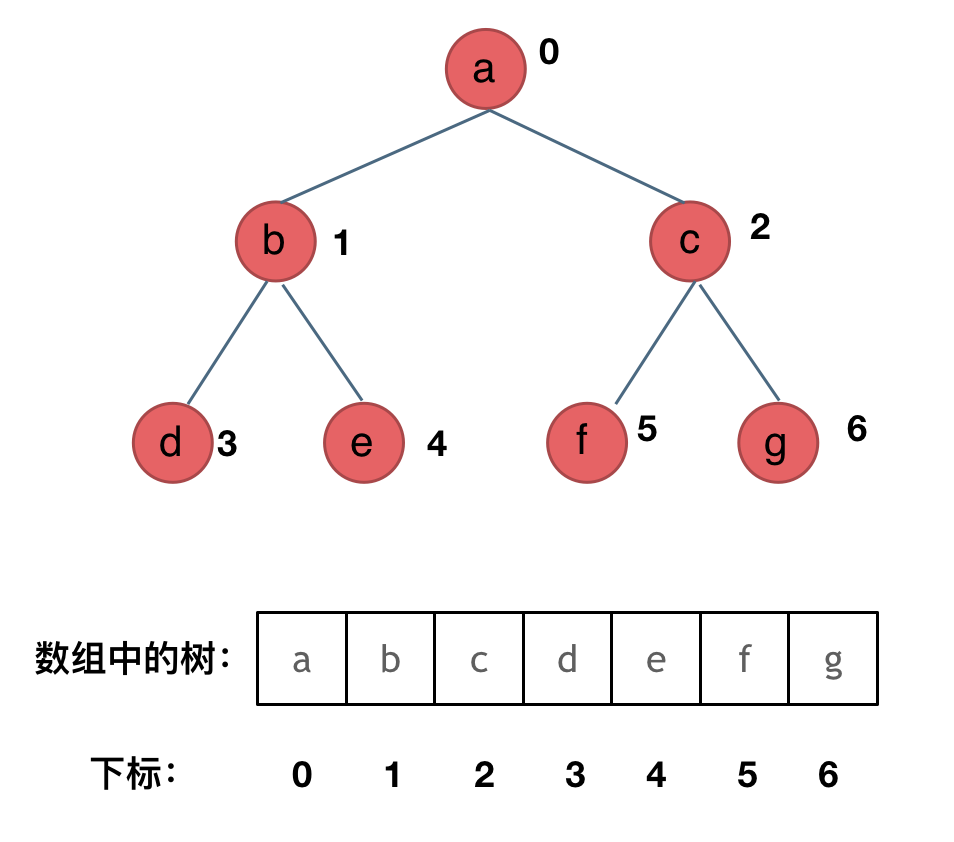
|
||||
|
||||
如果父节点的数组下标是 `i`,那么它的左孩子就是 `i * 2 + 1`,右孩子就是 `i * 2 + 2`。
|
||||
|
||||
## 遍历方式
|
||||
|
||||
- 深度优先遍历
|
||||
- 前序遍历(递归法,迭代法)
|
||||
- 中序遍历(递归法,迭代法)
|
||||
- 后序遍历(递归法,迭代法)
|
||||
- 广度优先遍历
|
||||
- 层序遍历(迭代法)
|
||||
|
||||
深度优先遍历:
|
||||
|
||||
1. 不保留全部节点状态,占用空间小
|
||||
2. 有回溯操作(即有入栈、出栈操作),运行速度慢
|
||||
3. 深度很大的情况下效率不高
|
||||
|
||||
广度优先遍历:
|
||||
|
||||
1. 保留全部节点状态,占用空间大
|
||||
2. 无回溯操作(即无入栈、出栈操作),运行速度快
|
||||
3. 对于解决最短或最少问题特别有效,而且寻找深度小(每个结点只访问一遍,结点总是以最短路径被访问,所以第二次路径确定不会比第一次短)
|
||||
|
||||
区分前中后序遍历的方法:
|
||||
|
||||
- 前序遍历:中左右
|
||||
- 中序遍历:左中右
|
||||
- 后序遍历:左右中
|
||||
|
||||
## 技巧
|
||||
|
||||
1. 深度优先搜索从下往上,广度优先搜索从上往下,所以如果需要处理从上往下并且状态积累的情形 (e.g. [s0404](https://leetcode.cn/problems/sum-of-left-leaves/) && [s0257](https://leetcode.cn/problems/binary-tree-paths/)) 可以先创建一个结构体用来描述节点状态,然后用 BFS 遍历。
|
||||
2. 写递归时,如果 `TreeNode *ptr` 不足以描述当前节点状态,则可以写一个辅助函数,接收 `TreeNode *ptr` 为参数,返回 `TreeNodeState` 来描述当前节点的状态。参考 [s0098](https://leetcode.cn/problems/validate-binary-search-tree/)
|
||||
3. 另一种需要结构体的地方是需要获得每个节点路径(即根节点到当前节点所经过的路径),可以用 DFS 或 BFS 遍历。
|
||||
4. 如果要处理不是从上往下积累状态,而是按照一定规则遍历节点并积累状态的情况(e.g. [s0538](https://leetcode.cn/problems/convert-bst-to-greater-tree/description/))则考虑用三种递归遍历方式中的一种来遍历,并用一个全局变量来记录遍历状态。另外,务必理解并记忆每种遍历方式的动态图!
|
||||
@@ -1,171 +0,0 @@
|
||||
# 遍历
|
||||
|
||||
## 深度优先遍历(递归法)
|
||||
|
||||
```cpp
|
||||
// para_n 用来描述每个节点的状态
|
||||
// 比如 para1 可以是当前节点的指针,para2 和 para3 可以用来表示当前指针的其它状态信息
|
||||
// 遍历结果可以用指针放在接收参数保存,也可以通过声明一个 class 的成员来保存
|
||||
void dfs(int para1, int para2, int para3, std::vector<std::string> &result) {
|
||||
// 讨论边界条件
|
||||
// 只需要在这里讨论结束条件即可,初始化的工作会在 dfs 外完成
|
||||
if (/* end condition */) {
|
||||
/* statement */
|
||||
}
|
||||
// 当当前节点状态越界或不合法时,剪枝
|
||||
if (/* invalid */) {
|
||||
return;
|
||||
}
|
||||
// 当当前节点状态合法时,遍历当前节点的所有子节点
|
||||
dfs(/* state of child node 1 */, result);
|
||||
dfs(/* state of child node 2 */, result);
|
||||
dfs(/* state of child node 3 */, result);
|
||||
}
|
||||
|
||||
void main(void) {
|
||||
dfs(/* state of root node */, /* initial result */);
|
||||
}
|
||||
```
|
||||
|
||||
前中后序遍历的区别就在于访问节点的顺序不同。
|
||||
|
||||
**注意**:务必理解和记忆每种遍历的遍历动态图!
|
||||
|
||||
前序遍历:
|
||||
|
||||
```cpp
|
||||
printf("%d\n", curNode->val);
|
||||
dfs(curNode->left, result);
|
||||
dfs(curNode->right, result);
|
||||
```
|
||||
|
||||

|
||||
|
||||
中序遍历:
|
||||
|
||||
```cpp
|
||||
dfs(curNode->left, result);
|
||||
printf("%d\n", curNode->val);
|
||||
dfs(curNode->right, result);
|
||||
```
|
||||
|
||||

|
||||
|
||||
后序遍历:
|
||||
|
||||
```cpp
|
||||
dfs(curNode->left, result);
|
||||
dfs(curNode->right, result);
|
||||
printf("%d\n", curNode->val);
|
||||
```
|
||||
|
||||

|
||||
|
||||
## 深度优先遍历(迭代法)
|
||||
|
||||
由于递归本质是对栈进行操作,因此也可以用迭代+栈的方式实现。
|
||||
|
||||
以中序遍历为例:
|
||||
|
||||
```cpp
|
||||
vector<int> inorderTraversal(TreeNode* root) {
|
||||
// 初始化结果集
|
||||
vector<int> result;
|
||||
// 初始化栈
|
||||
stack<TreeNode*> st;
|
||||
// 当根节点不为空时将根节点入栈
|
||||
if (root != NULL) st.push(root);
|
||||
// 当栈为空时停止迭代
|
||||
while (!st.empty()) {
|
||||
// 先获取栈顶元素
|
||||
TreeNode* node = st.top();
|
||||
// 栈顶元素出栈
|
||||
st.pop();
|
||||
// 如果栈顶元素不为空指针,则将节点按顺序入栈
|
||||
if (node != NULL) {
|
||||
// 注意是右中左,和左中右反着,因为栈是先进后出
|
||||
// 右
|
||||
if (node->right) st.push(node->right);
|
||||
// 中
|
||||
st.push(node);
|
||||
st.push(NULL);
|
||||
// 左
|
||||
if (node->left) st.push(node->left);
|
||||
} else { // 只有遇到空节点的时候,才将下一个节点放进结果集
|
||||
node = st.top(); // 重新取出栈中元素
|
||||
st.pop();
|
||||
result.push_back(node->val); // 加入到结果集
|
||||
}
|
||||
}
|
||||
return result;
|
||||
}
|
||||
```
|
||||
|
||||
## 广度优先遍历(层序遍历)
|
||||
|
||||
```cpp
|
||||
void iter(Node *root) {
|
||||
// 讨论边界条件
|
||||
if (root == nullptr) {
|
||||
return;
|
||||
}
|
||||
// 初始化一个队列
|
||||
std::queue<Node *> queue;
|
||||
// 把根节点放进去
|
||||
// 这里要检查一下是否为空,也就是先检查边界条件再操作
|
||||
// DFS 不需要检查边界条件就可以直接操作,这是因为边界条件在下一层迭代中检查
|
||||
if (root) queue.push(root);
|
||||
// 开始迭代,当队列为空时结束迭代
|
||||
while (!queue.empty()) {
|
||||
// 取队首
|
||||
Node *node = queue.front();
|
||||
// 弹出队首
|
||||
queue.pop();
|
||||
// 将队首的值放进向量中
|
||||
vec.push_back(node->val);
|
||||
// 遍历队首的所有子节点并把它们放到队尾
|
||||
if (node->left) queue.push(node->left);
|
||||
if (node->right) queue.push(node->right);
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
如果需要对每一层进行处理,则修改如下:
|
||||
|
||||
```cpp
|
||||
vector<vector<int>> iter(Node *root) {
|
||||
// 讨论边界条件
|
||||
if (root == nullptr) {
|
||||
return;
|
||||
}
|
||||
// 初始化一个队列
|
||||
std::queue<Node *> queue;
|
||||
// 初始化结果向量
|
||||
vector<vector<int>> result;
|
||||
// 把根节点放进去
|
||||
if (root) queue.push(root);
|
||||
// 开始迭代,当队列为空时结束迭代
|
||||
while (!queue.empty()) {
|
||||
// 获得当前层的节点个数
|
||||
int size = queue.size();
|
||||
// 创建一个向量用来装当前层的结果
|
||||
vector<int> vec;
|
||||
// 开始迭代当前层
|
||||
for (int i{0}; i < size; ++i) {
|
||||
// 取队首
|
||||
Node *node = queue.front();
|
||||
// 弹出队首
|
||||
queue.pop();
|
||||
// 将队首的值放进向量中
|
||||
vec.push_back(node->val);
|
||||
// 遍历队首的所有子节点并把它们放到队尾
|
||||
if (node->left) queue.push(node->left);
|
||||
if (node->right) queue.push(node->right);
|
||||
}
|
||||
result.push_back(vec);
|
||||
}
|
||||
return result;
|
||||
}
|
||||
```
|
||||
|
||||
如果需要找某一层的什么节点的话,考虑用这个版本的层序遍历。
|
||||
@@ -1,7 +0,0 @@
|
||||
# 棋盘问题
|
||||
|
||||
棋盘问题:N 皇后,解数独等等
|
||||
|
||||
## [51. N 皇后](https://leetcode.cn/problems/n-queens/)
|
||||
|
||||
## [37. 解数独](https://leetcode.cn/problems/sudoku-solver/)
|
||||
@@ -1,161 +0,0 @@
|
||||
# 组合问题
|
||||
|
||||
组合问题:N 个数里面按一定规则找出 k 个数的集合
|
||||
|
||||
## [77. 组合](https://leetcode.cn/problems/combinations/description/)
|
||||
|
||||

|
||||
|
||||
每个节点存储的数据是什么?是一个 `vector<int>` 类型的数据,代表当前节点的路径。
|
||||
|
||||
下一个节点的路径需要基于上一个节点的路径来获得,因此传入参数应该有一个 `vector<int> path`。另外,还需要有一个 `vector<vector<int>> &result` 用来存放结果。
|
||||
|
||||
终止条件是什么?回溯法中的每个节点并不是真的树状节点,没有 `nullptr` ,因此用空指针来判断是否到了叶子节点并不合理。
|
||||
|
||||
本题中我们可以通过高度来判断是否达到了叶子节点,如果 `path.size() == k` 则说明到达了叶子节点,则停止迭代,并把当前路径添加到结果变量中。
|
||||
|
||||
因此我们还需要高度 `k`,`int k` 也应该是一个传入参数。
|
||||
|
||||
为了防止重复,我们需要在 `[1, n]` 中的一个子区间 `[begin, n]` 中选择一个数,`[1, begin]` 是我们已经选过了的,因此我们需要 `int n` 和 `int begin` 来作为传入参数。
|
||||
|
||||
在每次迭代中,我们从 `[begin, n]` 中挨个选一个数加到上一轮迭代传递进来的 `path` 中,然后进行下一轮迭代。
|
||||
|
||||
```cpp
|
||||
void combineDFS(int n, int k, int begin, vector<int> &path,
|
||||
vector<vector<int>> &result) {
|
||||
// 当 path 长度等于 k 时停止迭代,并将加入结果
|
||||
if (path.size() == k) {
|
||||
result.push_back(path);
|
||||
return;
|
||||
}
|
||||
|
||||
// 遍历可能的搜索起点
|
||||
for (int i = begin; i <= n; ++i) {
|
||||
// 将 i 加入路径
|
||||
path.push_back(i);
|
||||
// 下一轮搜索
|
||||
combineDFS(n, k, i + 1, path, result);
|
||||
// 回溯,撤销处理的节点
|
||||
path.pop_back();
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
我们现在来看看能不能优化。
|
||||
|
||||

|
||||
|
||||
在上图的这种情况中,每一层其实都可以剪掉一些不可能的分支,我们可以对每一层循环的终止条件进行限制,从而剪枝。
|
||||
|
||||
优化后的代码如下:
|
||||
|
||||
```cpp
|
||||
void combineDFS(int n, int k, int begin, vector<int> &path,
|
||||
vector<vector<int>> &result) {
|
||||
// 当 path 长度等于 k 时停止迭代,并将加入结果
|
||||
if (path.size() == k) {
|
||||
result.push_back(path);
|
||||
return;
|
||||
}
|
||||
|
||||
// 遍历可能的搜索起点
|
||||
// 在这一步中,每一次循环都可以对末尾进行限制来剪枝
|
||||
for (int i = begin; i <= n - (k - path.size()) + 1; ++i) {
|
||||
// 将 i 加入路径
|
||||
path.push_back(i);
|
||||
// 下一轮搜索
|
||||
combineDFS(n, k, i + 1, path, result);
|
||||
// 回溯,撤销处理的节点
|
||||
path.pop_back();
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
## [216. 组合总和 III](https://leetcode.cn/problems/combination-sum-iii/)
|
||||
|
||||
## [39. 组合总和](https://leetcode.cn/problems/combination-sum/)
|
||||
|
||||
## [40. 组合总和 II](https://leetcode.cn/problems/combination-sum-ii/)
|
||||
|
||||
最难的一个组合总和,因为 `candidates` 有重复元素,而要求最终结果不能重复。
|
||||
|
||||
e.g. 1
|
||||
|
||||
```text
|
||||
Input: candidates = [10,1,2,7,6,1,5], target = 8
|
||||
Output:
|
||||
[
|
||||
[1,1,6],
|
||||
[1,2,5],
|
||||
[1,7],
|
||||
[2,6]
|
||||
]
|
||||
```
|
||||
|
||||
如果你只是单纯地在 s0039 的基础上在下一次递归中将 `startIndex` 设为 `i + 1` 那么最终结果就会出现两个 `[1, 2, 5]`。
|
||||
|
||||
如果你直接排除 `candidates[i] == candidates[i - 1]` 的情形,那么最终结果就没有 `[1, 1, 6]`。
|
||||
|
||||
正确的逻辑应该是如果 `candidates[i] == candidates[i - 1]` 且 `candidates[i - 1]` 使用过,则剪枝。
|
||||
|
||||

|
||||
|
||||
那么我们现在要来定义一下什么叫“使用过”。这张图里面有两种“使用过”,第一种使用过是“在树枝上使用过”,第二种使用过是“在数层上使用过”。
|
||||
|
||||
第一种“使用过”显然是合法的,我们允许元素在一条树枝上重复出现。而第二种“使用过”是不合法的,生成的结果重复了。
|
||||
|
||||
因此我们只需要对第二种“使用过”进行剪枝,而保留第一种“使用过”。
|
||||
|
||||
怎么做呢?我们创建一个 `vector<bool> used` 用来记录元素是否在树枝上出现过,初始化为 `false`。
|
||||
|
||||
```cpp
|
||||
used[i] = true;
|
||||
combinationSum2DFS(candidates, target, i + 1, path, sum + candidates[i],
|
||||
used, result);
|
||||
used[i] = false;
|
||||
```
|
||||
|
||||
那么 `used[i - 1] == true` 说明 `candidates[i - 1]` 在树枝上出现过,我们需要保留这种情况,不剪枝。
|
||||
|
||||
```cpp
|
||||
// 剪枝,但保留树枝重复的情况
|
||||
if (i > 0 && candidates[i] == candidates[i - 1] && used[i - 1] == false)
|
||||
continue;
|
||||
```
|
||||
|
||||
另外需要注意一点,为了进行剪枝,我们需要对 `candidates` 进行排序:
|
||||
|
||||
```cpp
|
||||
// 对 candidates 进行升序排序,这是为了进行剪枝
|
||||
sort(candidates.begin(), candidates.end());
|
||||
```
|
||||
|
||||
完整代码如下:
|
||||
|
||||
```cpp
|
||||
void combinationSum2DFS(vector<int> &candidates, int target, int startIndex,
|
||||
vector<int> &path, int sum, vector<bool> &used,
|
||||
vector<vector<int>> &result) {
|
||||
// 结束条件:总和等于 target 。不存在总和大于 target 的情况,因为已经被剪枝了
|
||||
if (sum == target) {
|
||||
result.push_back(path);
|
||||
return;
|
||||
}
|
||||
|
||||
// 开始迭代
|
||||
int size = candidates.size();
|
||||
for (int i = startIndex; i < size; ++i) {
|
||||
// 剪枝,当现在节点的 sum 已经超过了 target,就没必要继续迭代了
|
||||
if (sum + candidates[i] > target) break;
|
||||
// 剪枝,但保留树枝重复的情况
|
||||
if (i > 0 && candidates[i] == candidates[i - 1] && used[i - 1] == false)
|
||||
continue;
|
||||
path.push_back(candidates[i]);
|
||||
used[i] = true;
|
||||
combinationSum2DFS(candidates, target, i + 1, path, sum + candidates[i],
|
||||
used, result);
|
||||
used[i] = false;
|
||||
path.pop_back();
|
||||
}
|
||||
}
|
||||
```
|
||||
@@ -1,52 +0,0 @@
|
||||
# 基础问题
|
||||
|
||||
## [509. 斐波那契数](https://leetcode.cn/problems/fibonacci-number/)
|
||||
|
||||
1. `dp[i]` 是第 `i` 个斐波那契数的数值
|
||||
2. `dp[i] = dp[i - 1] + dp[i - 2]`
|
||||
3. `dp[0] = 0`, `dp[1] = 1`
|
||||
4. 从前向后遍历
|
||||
|
||||
## [70. 爬楼梯](https://leetcode.cn/problems/climbing-stairs/)
|
||||
|
||||
1. `dp[i]` 是爬到第 `i` 阶楼梯的方法数
|
||||
2. `dp[i] = dp[i - 1] + dp[i - 2]`
|
||||
3. `dp[1] = 1`, `dp[2] = 2`, `dp[0]` 不用管
|
||||
4. 从前向后遍历
|
||||
|
||||
## [746. 使用最小花费爬楼梯](https://leetcode.cn/problems/min-cost-climbing-stairs/)
|
||||
|
||||
1. `dp[i]` 是爬到第 `i` 阶的最小开销(假设 `i == 0` 代表第一个阶梯)
|
||||
2. `dp[i] = min{dp[i - 1] + cost[i - 1], dp[i - 2] + cost[i - 2]}`
|
||||
3. `dp[0] = 0`, `dp[1] = 0`
|
||||
4. 从前向后遍历
|
||||
|
||||
## [62. 不同路径](https://leetcode.cn/problems/unique-paths/)
|
||||
|
||||
1. `dp[i][j]` 表示到 `(i, j)` 的位置有多少种路径(从 `(0, 0)` 出发)
|
||||
2. `dp[i][j] = dp[i - 1][j] + dp[i][j - 1]`
|
||||
3. `dp[i][0] = 1`, `dp[0][j] = 1`
|
||||
4. 从前向后遍历
|
||||
|
||||
## [63. 不同路径 II](https://leetcode.cn/problems/unique-paths-ii/)
|
||||
|
||||
1. `dp[i][j]` 表示到 `(i, j)` 的位置有多少种路径(从 `(0, 0)` 出发)
|
||||
2. `dp[i][j] = if (isNotObstacle[i - 1][j]) dp[i - 1][j] + if (isNotObstacle[i][j - 1]) dp[i][j - 1]`
|
||||
3. 如果 `(i, 0)` 是障碍物,那么 `(0, 0)` 到 `(i - 1, 0)` 都初始化为 `1`,后面的初始化为 `0`。`(0, j)` 同理
|
||||
4. 从前向后遍历
|
||||
|
||||
## [343. 整数拆分](https://leetcode.cn/problems/integer-break/)
|
||||
|
||||
1. `dp[i]` 为分拆数字 `i`,可以得到的最大乘积
|
||||
2. `dp[i] = max{dp[i], (i - j) * j, dp[i - j] * j}`
|
||||
3. `dp[2] = 1`
|
||||
4. 从前向后遍历
|
||||
|
||||
## [96. 不同的二叉搜索树](https://leetcode.cn/problems/unique-binary-search-trees/)
|
||||
|
||||
1. `dp[i]` 为 `n == i` 时二叉搜索树的个数
|
||||
2. `dp[i] += dp[j - 1] * dp[i - j]`,`j - 1` 为 `j` 为头结点左子树节点数量,`i - j` 为以 `j` 为头结点右子树节点数量
|
||||
3. `dp[0] = 1` 空节点也是一棵二叉树,也是一棵二叉搜索树
|
||||
4. 从前向后遍历
|
||||
|
||||
找规律
|
||||
@@ -1,22 +0,0 @@
|
||||
# 总结
|
||||
|
||||
和贪心相似,从将问题划分为多个子问题,最后得出最终问题的解,但是区别在于每一步之间涉及到状态推导,下一步是基于上一步的结果和之前的记忆(也就是上上次,上上上次等的结果)经过一定逻辑推导得出的。
|
||||
|
||||
分五步:
|
||||
|
||||
1. 确定 `dp[i]` 是什么
|
||||
2. 确定递推公式
|
||||
3. `dp` 数组如何初始化
|
||||
4. 确定遍历顺序(从前向后还是从后向前)和范围
|
||||
5. 推几个来验证
|
||||
|
||||
如何确定遍历顺序?除了背包问题外,一般减法从前往后,加法从后往前。参考子序列问题——回文串。
|
||||
|
||||
为什么一般是这样?你遍历几个试试看就知道了。
|
||||
|
||||
如何确定初始化方法?确定了遍历顺序以及遍历范围后,再遍历几个试试。
|
||||
|
||||
技巧:
|
||||
|
||||
- 如果可以的话,初始化 `dp` 的长度,而不要每次都 `dp.push_back()`。初始化能够有更好的性能。
|
||||
- 知道用 DP ,也知道 `dp[i]` 应该用来表示什么,但不知道递推关系。这个时候多举几个简单的例子找规律(s0096)。
|
||||
@@ -1,11 +0,0 @@
|
||||
# 四数相加 II
|
||||
|
||||
[Leetcode](https://leetcode.com/problems/4sum-ii/)
|
||||
|
||||
这是一道经典的哈希表的题。
|
||||
|
||||
双重循环遍历 A 和 B ,把 `A[i] + B[j]` 作为 key ,把出现的次数作为 value 。
|
||||
|
||||
同样地遍历 C 和 D 。
|
||||
|
||||
那么现在就得到了两个哈希表了,遍历哈希表,看看是否有两个值之和为 0 ,如果有的话统计出现的次数。
|
||||
@@ -1,152 +0,0 @@
|
||||
# 总结
|
||||
|
||||
使用场景:手动模拟一下感觉可以局部最优推出整体最优,而且想不到反例,那么就试一试贪心。
|
||||
|
||||
思路:
|
||||
|
||||
假设题干是这样的:给出一系列元素(通常放在一个数组中),请你从中挑选出满足条件的 N 个数,使得总和最大。
|
||||
|
||||
来分析一下题干:
|
||||
|
||||
- 一系列元素,这是 base
|
||||
- 满足条件的 N 个数,这是限制条件
|
||||
- 总和最大,这是全局最优的优化目标
|
||||
|
||||
贪心算法是怎样的呢?就是直接找全局最优一般不好找,我们可以在 base 上找局部最优,比如我们可以这么设计:
|
||||
|
||||
- 总和大于 0 的一段连续子数组,这是限制条件
|
||||
- 长度最长,这是局部最优的优化目标
|
||||
|
||||
限制条件和优化目标都不一定要和全局最优一样,但是这里有个关键:
|
||||
|
||||
你在找局部最优的过程中可以推导出全局最优。
|
||||
|
||||
注意,不是从所有局部最优的结果中推导出全局最优的结果,而是你在寻找局部最优的过程中可以找到全局最优。
|
||||
|
||||
什么意思?
|
||||
|
||||
假设你找到了 K 个局部最优结果,但我们并不是要从这 K 个结果中推出全局最优,而是在你找这 K 个结果的过程中,我们可以用一个变量 `record` 来记录某些东西,然后由这个变量 `record` 和这 K 个局部最优结果共同推导出全局最优解。
|
||||
|
||||
---
|
||||
|
||||
## [53. 最大子序和](https://leetcode.cn/problems/maximum-subarray/)
|
||||
|
||||
> Given an integer array `nums`, find the subarray with the largest sum, and return its _sum_.
|
||||
>
|
||||
> ```text
|
||||
> Input: nums = [-2,1,-3,4,-1,2,1,-5,4]
|
||||
> Output: 6
|
||||
> Explanation: The subarray [4,-1,2,1] has the largest sum 6.
|
||||
> ```
|
||||
|
||||
全局:
|
||||
|
||||
- 限制:连续子数组
|
||||
- 目标:总和最大
|
||||
|
||||
局部:
|
||||
|
||||
- 限制:连续子数组,总和大于零
|
||||
- 目标:该子数组长度最长
|
||||
|
||||
过程:
|
||||
|
||||
在找最长子数组时用一个变量 `count` 记录当前总和,用一个变量 `max` 记录最大总和。
|
||||
|
||||
- `if (count > max) max = count`
|
||||
- `if (count < 0) count = 0`
|
||||
|
||||
## [122. 买卖股票的最佳时机 II](https://leetcode.cn/problems/best-time-to-buy-and-sell-stock-ii/)
|
||||
|
||||
> You are given an integer array `prices` where `prices[i]` is the price of a given stock on the `ith` day.
|
||||
>
|
||||
> On each day, you may decide to buy and/or sell the stock. You can only hold **at most one share** of the stock at any time. However, you can buy it then immediately sell it on the **same day**.
|
||||
>
|
||||
> Find and return the **_maximum_** profit you can achieve.
|
||||
>
|
||||
> ```text
|
||||
> Input: prices = [7,1,5,3,6,4]
|
||||
> Output: 7
|
||||
> Explanation: Buy on day 2 (price = 1) and sell on day 3 (price = 5), profit = 5-1 = 4.
|
||||
> Then buy on day 4 (price = 3) and sell on day 5 (price = 6), profit = 6-3 = 3.
|
||||
> Total profit is 4 + 3 = 7.
|
||||
> ```
|
||||
|
||||
全局目标:总利润最大
|
||||
|
||||
局部目标:最长上升区间
|
||||
|
||||
过程:找到每个最长上升区间,将每个上升区间的利润加起来就是总利润了。
|
||||
|
||||
## [55. 跳跃游戏](https://leetcode.cn/problems/jump-game/)
|
||||
|
||||
> You are given an integer array `nums`. You are initially positioned at the array's **first index**, and each element in the array represents your maximum jump length at that position.
|
||||
>
|
||||
> Return `true` _if you can reach the last index_, or `false` _otherwise_.
|
||||
>
|
||||
> ```text
|
||||
> Input: nums = [2,3,1,1,4]
|
||||
> Output: true
|
||||
> Explanation: Jump 1 step from index 0 to 1, then 3 steps to the last index.
|
||||
> ```
|
||||
|
||||
全局最优:找到最长覆盖距离
|
||||
|
||||
局部最优:找到当前区间的最长覆盖距离
|
||||
|
||||
过程:一开始第一个元素的值就是初始覆盖区间的长度,遍历这个区间的所有元素,看看能不能找到能延长当前区间覆盖距离的元素,并延长区间覆盖距离,这样一直迭代,看它能不能到达数组末尾。
|
||||
|
||||
## [45. 跳跃游戏 II](https://leetcode.cn/problems/jump-game-ii/)
|
||||
|
||||
> You are given a **0-indexed** array of integers `nums` of length `n`. You are initially positioned at `nums[0]`.
|
||||
>
|
||||
> Each element `nums[i]` represents the maximum length of a forward jump from index `i`. In other words, if you are at `nums[i]`, you can jump to any `nums[i + j]` where:
|
||||
>
|
||||
> - `0 <= j <= nums[i]` and
|
||||
> - `i + j < n`
|
||||
>
|
||||
> Return _the minimum number of jumps to reach_ `nums[n - 1]`. The test cases are generated such that you can reach `nums[n - 1]`.
|
||||
|
||||
全局最优:找到最短步数达到最长覆盖距离
|
||||
|
||||
局部最优:找到当前覆盖区间的元素,使得能最大程度地延长当前覆盖范围。
|
||||
|
||||
过程:一开始第一个元素的值就是初始覆盖区间的长度,遍历这个区间的所有元素,找到这样一个元素,它能够最大程度地延长当前覆盖区间,这个元素就是下一跳。在下一个覆盖区间中,再找到同样的元素,这样一直迭代。
|
||||
|
||||
## [452. 用最少数量的箭引爆气球](https://leetcode.cn/problems/minimum-number-of-arrows-to-burst-balloons/)
|
||||
|
||||
全局:
|
||||
|
||||
- 限制:射完全部气球
|
||||
- 目标:消耗的箭的数量最少
|
||||
|
||||
局部:
|
||||
|
||||
- 限制:射箭的范围是当前气球所在的范围
|
||||
- 目标:这一箭要射穿的气球数量达到最大
|
||||
|
||||
算法优化:先对左边界(或右边界)进行排序,以降低时间复杂度。
|
||||
|
||||
## [435. 无重叠区间](https://leetcode.cn/problems/non-overlapping-intervals/)
|
||||
|
||||
从左向右记录非交叉区间的个数,用区间总数减去非交叉区间的个数就是需要移除的区间个数了。问题就是要求非交叉区间的最大个数。
|
||||
|
||||
先按右边界进行排序。
|
||||
|
||||
局部最优:优先选右边界小的区间,所以从左向右遍历,留给下一个区间的空间大一些,从而尽量避免交叉。
|
||||
|
||||
全局最优:选取最多的非交叉区间。
|
||||
|
||||
## [56. 合并区间](https://leetcode.cn/problems/merge-intervals/)
|
||||
|
||||
先按左边界排序。
|
||||
|
||||
局部最优:当前区间能合并出的最长区间
|
||||
|
||||
全局最优:合并所有重叠区间
|
||||
|
||||
## [968. 监控二叉树](https://leetcode.cn/problems/binary-tree-cameras/)
|
||||
|
||||
局部最优:让叶子节点的父节点安摄像头,所用摄像头最少
|
||||
|
||||
全局最优:全部摄像头数量所用最少
|
||||
@@ -1,11 +0,0 @@
|
||||
# 总结
|
||||
|
||||
当我们需要判断某个元素是否出现过时,考虑用哈希表。
|
||||
|
||||
## unordered_map 与 unordered_set
|
||||
|
||||
这俩的底层都是用哈希函数实现的,因此访问其中的元素可以达到 O(1) 的时间复杂度。
|
||||
|
||||
它们的区别在于,unordered_map 存储的是 key-value ,而 unordered_set 只存储 key 。
|
||||
|
||||
一般我们直接用 unordered_map 就可以完成所有操作了。
|
||||
@@ -1,31 +0,0 @@
|
||||
# 打家劫舍
|
||||
|
||||
## [198. 打家劫舍](https://leetcode.cn/problems/house-robber/)
|
||||
|
||||
- `dp[i]` 为考虑下标i(包括i)以内的房屋,最多可以偷窃的金额为
|
||||
- `dp[i] = max{dp[i - 2] + dp[i], dp[i - 1]}`
|
||||
- `dp[0] = nums[0]`, `dp[1] = max{nums[0], nums[1]}`, 其它为 `0`
|
||||
- 从前向后遍历
|
||||
|
||||
## [213. 打家劫舍II](https://leetcode.cn/problems/house-robber-ii/)
|
||||
|
||||
和 s0198 差不多,只不过需要考虑三种情况:
|
||||
|
||||
1. 只偷 `nums[0...i-1]`
|
||||
2. 只偷 `nums[1...i]`
|
||||
3. 只偷 `nums[1...i-1]`
|
||||
|
||||
这三种情况取最大值即可。
|
||||
|
||||
## [337. 打家劫舍 III](https://leetcode.cn/problems/house-robber-iii/)
|
||||
|
||||
递归遍历,递归函数的返回值是一个长度为 2 的数组,第一个元素为偷当前节点能偷到的最多的钱,第二个元素为不偷当前节点能够偷到的最多的钱。
|
||||
|
||||
```cpp
|
||||
vector<int> left = robTree(cur->left); // 左
|
||||
vector<int> right = robTree(cur->right); // 右
|
||||
|
||||
/*
|
||||
然后在这里动态规划
|
||||
*/
|
||||
```
|
||||
@@ -1,56 +0,0 @@
|
||||
# 用栈实现队列 && 用队列实现栈
|
||||
|
||||
## 用栈实现队列
|
||||
|
||||
[Leetcode](https://leetcode.com/problems/implement-queue-using-stacks/)
|
||||
|
||||
「输入栈」会把输入顺序颠倒;如果把「输入栈」的元素逐个弹出放到「输出栈」,再从「输出栈」弹出元素的时候,则可以负负得正,实现了先进先出。
|
||||
|
||||
```cpp
|
||||
#include <stack>
|
||||
|
||||
class MyQueue {
|
||||
public:
|
||||
std::stack<int> *inStack, *outStack;
|
||||
|
||||
MyQueue() {
|
||||
inStack = new std::stack<int>;
|
||||
outStack = new std::stack<int>;
|
||||
}
|
||||
|
||||
void transfer(void) {
|
||||
if (outStack->empty()) {
|
||||
while (!inStack->empty()) {
|
||||
outStack->push(inStack->top());
|
||||
inStack->pop();
|
||||
}
|
||||
}
|
||||
}
|
||||
|
||||
void push(int x) { inStack->push(x); }
|
||||
|
||||
int pop() {
|
||||
transfer();
|
||||
int val = outStack->top();
|
||||
outStack->pop();
|
||||
return val;
|
||||
}
|
||||
|
||||
int peek() {
|
||||
transfer();
|
||||
return outStack->top();
|
||||
}
|
||||
|
||||
bool empty() { return inStack->empty() && outStack->empty(); }
|
||||
};
|
||||
```
|
||||
|
||||
## 用队列实现栈
|
||||
|
||||
[Leetcode](https://leetcode.com/problems/implement-stack-using-queues/)
|
||||
|
||||
一个队列为主队列,一个为辅助队列,当入栈操作时,我们先将主队列内容导入辅助队列,然后将入栈元素放入主队列队头位置,再将辅助队列内容,依次添加进主队列即可。
|
||||
|
||||
```cpp
|
||||
|
||||
```
|
||||
@@ -1,3 +0,0 @@
|
||||
# KMP
|
||||
|
||||
[Blog](https://www.sainnhe.dev/post/kmp/)
|
||||
@@ -1,296 +0,0 @@
|
||||
# 背包问题
|
||||
|
||||
## 01 背包
|
||||
|
||||
有 `n` 件物品和一个最多能背重量为 `knapsackWeight` 的背包。
|
||||
|
||||
第 `i` 件物品的重量是 `weight[i]`,其价值是 `value[i]`,它们都是正整数。
|
||||
|
||||
每件物品只能用一次,求解将哪些物品装入背包里物品价值总和最大。
|
||||
|
||||
- `dp[i][j]` 表示从下标为 `[0 - i]` 的物品里任意取,放进容量为 `j` 的背包,价值总和最大是多少。
|
||||
- 递推公式:
|
||||
- 不放物品 `i`:`dp[i - 1][j]`
|
||||
- 放物品 `i`:`dp[i - 1][j - weight[i]] + value[i]`
|
||||
- 这两种情况选价值最大的那个,即 `dp[i][j] = max{dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]}`
|
||||
- 初始化
|
||||
- `dp[i][0] = 0` 即当前背包能装的重量为 `0`,就是什么都装不下,当然价值为 `0`
|
||||
- `dp[0][j]`
|
||||
- `if (j < weight[0])`, `dp[0][j] = 0` 背包装不下第 `0` 个物品
|
||||
- `if (j >= weight[0])`, `dp[0][j] = value[0]` 背包能装下第 `0` 个物品
|
||||
- `i = 0` 和 `j = 0` 的情况都初始化完了,因此我们写双重循环的时候 `i` 和 `j` 应该从 `1` 开始。
|
||||
- `i` 和 `j` 都从前往后遍历
|
||||
|
||||
```cpp
|
||||
void knapsack_problem_2d() {
|
||||
vector<int> weight = {1, 3, 4};
|
||||
vector<int> value = {15, 20, 30};
|
||||
int knapsackWeight = 4;
|
||||
|
||||
// 二维数组
|
||||
// 之所以初始化 j 的范围是 0 ~ knapsackWeight + 1 ,是因为我们会索引 dp[i][knapsackWeight]
|
||||
vector<vector<int>> dp(weight.size(), vector<int>(knapsackWeight + 1, 0));
|
||||
|
||||
// 初始化
|
||||
for (int j = weight[0]; j <= knapsackWeight; j++) {
|
||||
dp[0][j] = value[0];
|
||||
}
|
||||
|
||||
// 开始遍历
|
||||
for (int i = 1; i < weight.size(); i++) { // 遍历物品
|
||||
for (int j = 1; j <= knapsackWeight; j++) { // 遍历背包容量
|
||||
if (j < weight[i])
|
||||
dp[i][j] = dp[i - 1][j];
|
||||
else
|
||||
dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
|
||||
}
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
接下来优化我们的代码。
|
||||
|
||||
注意到递推公式的右侧只用到了 `dp[i - 1]`,我们可以把它看成是 `dp[i]` 上一步的状态,因此每一次迭代的时候我们完全可以将 `dp[i - 1]` 覆盖到 `dp[i]`,这样可以将二维数组压缩到一维。
|
||||
|
||||
递推公式可以修改成:`dp[j] = max{dp[j], dp[j - weight[i]] + value[i]}`
|
||||
|
||||
这就是滚动数组的思路,当上一层可以重复利用的时候,我们直接把上一层拷贝到当前层。从递推公式来看,只要递推公式满足了右侧只用了 `dp[i - 1]` 那么就可以压缩。
|
||||
|
||||
来分析 DP 的思路:
|
||||
|
||||
- `dp[j]` 表示第 `i` 层容量为 `j` 的背包所能背的物品的最大价值。
|
||||
- 递推公式:
|
||||
- `dp[j] = dp[j]`, `if j < weight[i]` 因为如果现在的物品重量比背包容量还大,那背包就装不下了,只能不装现在的这一个,那就是 `dp[i][j] = dp[i - 1][j]`,也就是 `dp[j] = dp[j]`
|
||||
- `dp[j] = max{dp[j], dp[j - weight[i]] + value[i]}`, `if j >= weight[i]` 这是能装下的情况
|
||||
- 总结一下就是只有当 `j >= weight[i]` 的时候我们才会调用第二个递推公式,否则 `dp[j]` 不变,于是我们可以将这一个放到第二层 for 循环里,第二层 for 循环的遍历范围是 `weight[i] <= j <= knapsackWeight`
|
||||
- 由于滚动数组每次都会覆盖上一层,因此初始化的时候我们只需要将滚动数组作为二维数组的第一层初始化
|
||||
- `dp[j]` 当 `j >= weight[0]` 时应该为 `value[0]` 也就是能装下第 `0` 个物品,否则为 `0`
|
||||
- 如果初始化了 `i = 0` 的第一层的话,那么双重 for 循环就应该从 `1` 开始。
|
||||
- 当你实际写代码的时候会发现,双重 for 循环可以用来初始化 `i = 0` 的情况,因此我们只需要初始化 `dp[j] = 0`,然后 `i` 从 `0` 开始就行。
|
||||
- 遍历顺序:
|
||||
- 物品 `i` 应该从前往后遍历
|
||||
- 但是背包重量 `j` 应该从后往前遍历
|
||||
|
||||
```cpp
|
||||
void knapsack_problem_1d() {
|
||||
vector<int> weight = {1, 3, 4};
|
||||
vector<int> value = {15, 20, 30};
|
||||
int knapsackWeight = 4;
|
||||
|
||||
// 初始化
|
||||
// 之所以初始化 j 的范围是 0 ~ knapsackWeight + 1 ,是因为我们会索引 dp[knapsackWeight]
|
||||
vector<int> dp(knapsackWeight + 1, 0);
|
||||
for (int i = 0; i < weight.size(); i++) { // 遍历物品
|
||||
for (int j = knapsackWeight; j >= weight[i]; j--) { // 遍历背包容量
|
||||
dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
|
||||
}
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
**Q: 能不能先遍历容量,再遍历物品?**
|
||||
|
||||
**A:** 不行,因为我们本来就是要用上一层的 `i - 1` 来覆盖这一层的 `i`。
|
||||
|
||||
**Q: 为啥二维不用从后往前呢?**
|
||||
|
||||
**A:** 因为 `dp[i][j]` 都是通过上一层即 `dp[i - 1][j]` 计算而来,本层的 `dp[i][j]` 并不会被覆盖。
|
||||
|
||||
**Q: 一维从后往前的本质是什么?**
|
||||
|
||||
**A:** 如果从后往前的话,`dp[j - weight[i]] + value[i]` 就用的是上一层的数据(这才是我们想要的),但如果从前往后的话,`dp[j - weight[i]] + value[i]` 就用的是这一层的数据,这将会导致物品被重复放进去。
|
||||
|
||||
**Q: 怎样初始化?**
|
||||
|
||||
**A:**
|
||||
|
||||
1. 先确定 `dp[j]` 应该初始化为多少,一般是 `0`
|
||||
2. 接下来确定 `dp[0]` 应该初始化为多少,我们直接看下一次访问到 `dp[0]` 时是什么情况就行,当访问到 `dp[0]` 时它应该是多少
|
||||
3. 我们接下来看看用当前的初始化值跑 `i = 0` 也就是第一层,逻辑是否正确。如果逻辑正确,那么第一层 for 循环的 `i` 就从 `0` 开始
|
||||
4. 如果不正确,我们专门对 `i = 0` 也就是第一层进行初始化,然后第一层 for 循环的 `i` 从 `1` 开始。
|
||||
|
||||
### [416. 分割等和子集](https://leetcode.cn/problems/partition-equal-subset-sum/)
|
||||
|
||||
二维数组:
|
||||
|
||||
- `dp[i][j]` 表示是否可以从 0 ~ i 选取一些元素,使得总和等于 j
|
||||
- 递推公式为:
|
||||
- `dp[i][j] = dp[i - 1][j] || dp[i - 1][j - nums[i]]`, `j >= nums[i]`
|
||||
- `dp[i][j] = dp[i - 1][j]`, `j < nums[i]`
|
||||
- 初始化:
|
||||
- `dp[0][j] = (j == nums[0])`
|
||||
- `dp[i][0] = false`
|
||||
- `i` 和 `j` 都从前往后
|
||||
|
||||
滚动数组:
|
||||
|
||||
- `dp[j]` 表示是否可以从 0 ~ i 选取一些元素,使得总和等于 j
|
||||
- 递推公式为:
|
||||
- `dp[j] = dp[j] || dp[j - nums[i]]`, `j >= nums[i]`
|
||||
- `dp[j] = dp[j]`, `j < nums[i]`
|
||||
- 因此第二层 for 循环的范围可以直接定成 `nums[i] <= j <= target`,然后调用第一个递推公式
|
||||
- 初始化:
|
||||
- `dp[j] = (j == nums[0])` 这是第一层也就是 `i == 0` 的情况
|
||||
- 这种情况可以写成默认初始化为 `false`,而 `dp[nums[0]] = true`
|
||||
- 遍历顺序:
|
||||
- `i` 从前往后,范围是 `1 <= i < length`
|
||||
- `j` 从后往前,范围是 `nums[i] <= j <= target`
|
||||
|
||||
本题中可以不初始化第一层,然后 `i` 从 0 开始。
|
||||
|
||||
### [1049. 最后一块石头的重量 II](https://leetcode.cn/problems/last-stone-weight-ii/)
|
||||
|
||||
仔细思考一下每个石头重量的加减方式,你会发现其实最终的重量可以这样表示:
|
||||
|
||||
`final = k0 * w0 + k1 * w1 + k2 * w2 + ...`
|
||||
|
||||
其中 `ki` 为 `+1` 或 `-1`,`wi` 为第 `i` 个石头的重量。
|
||||
|
||||
那么 `ki` 取负的所有石头重量之和我们表示为 `neg`,其它石头重量之和为 `total - neg`。
|
||||
|
||||
我们的目的就是要在 `neg <= total/2` 的前提下,让 `neg` 达到最大。
|
||||
|
||||
这就是一个 01 背包问题。
|
||||
|
||||
- `i` 对应石头下标,每个石头的重量为 `stones[i]`,价值为 `stones[i]`
|
||||
- `j` 对应背包容量,最大为 `total/2`
|
||||
|
||||
我们直接上滚动数组:
|
||||
|
||||
- `dp[j]` 表示从 0 ~ i 中选石头,放进容量为 `j` 的背包,所能达到的最大价值
|
||||
- 迭代公式:
|
||||
- `if (j < stones[i]) dp[j] = dp[j]`
|
||||
- `if (j >= stones[i]) dp[j] = max{dp[j], dp[j - stones[i]] + stones[i]}`
|
||||
- 第二层迭代的范围是 `stones[i] ~ total/2`
|
||||
- 初始化:
|
||||
- `if (j < stones[0]) dp[j] = 0`
|
||||
- `if (j >= stones[0]) dp[j] = stones[0]`
|
||||
- 遍历:
|
||||
- `i` 从 1 到 length - 1
|
||||
- `j` 从 `total/2` 向下取整,遍历到 `stones[i]`
|
||||
|
||||
本题中可以不初始化第一层,然后 `i` 从 0 开始。
|
||||
|
||||
## 完全背包
|
||||
|
||||
和 01 背包的区别就在于,01 背包的每个元素只能用一次,而完全背包的每个物品能够重复使用。
|
||||
|
||||
代码也很简单,我们知道 01 背包的第二层 for 循环是从大到小遍历,这是为了去重,而完全背包是可以重复添加物品的,因此要从小到大遍历
|
||||
|
||||
```cpp
|
||||
void complete_knapsack_problem_1d() {
|
||||
vector<int> weight = {1, 3, 4};
|
||||
vector<int> value = {15, 20, 30};
|
||||
int knapsackWeight = 4;
|
||||
|
||||
vector<int> dp(knapsackWeight + 1, 0);
|
||||
for (int i = 0; i < weight.size(); i++) { // 遍历物品
|
||||
for (int j = weight[i]; j <= knapsackWeight; j++) { // 遍历背包容量
|
||||
dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
|
||||
}
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
### [518. 零钱兑换 II](https://leetcode.cn/problems/coin-change-ii/)
|
||||
|
||||
- `dp[j]` 的含义是从 0 ~ i 这些硬币中选择,组合成总金额为 j 的组合数
|
||||
- `dp[j] += dp[j - coins[i]]`
|
||||
- 初始化:
|
||||
- 当 `i = 0` 的时候,也就是只有 `coins[0]` 这一种硬币的时候,当 `j` 可以被 `coins[0]` 整除的时候就赋值为 `1`,否则赋值为 `0`
|
||||
- 一种特殊情况是 `dp[0]`,它表示组合成总金额为 `0` 的组合数,我们必须把它赋值为 `1`,这是因为当我们执行 `dp[j] += dp[j - coins[i]]` 的时候,如果 `j == coins[i]` 那么显然应该自增 `1`。
|
||||
- 看看能不能不初始化第一层,我们直接删掉代码试试发现可以,那就不初始化第一层。
|
||||
- 遍历顺序都是从前向后
|
||||
|
||||
### [377. 组合总和 Ⅳ](https://leetcode.cn/problems/combination-sum-iv/)
|
||||
|
||||
这道题我们要先分清楚组合和排列。
|
||||
|
||||
`(1, 2)` 和 `(2, 1)` 是不同的排列,同样的组合。
|
||||
|
||||
本题求的是排列数。
|
||||
|
||||
**如果求组合数就是外层 for 循环遍历物品,内层 for 遍历背包;**
|
||||
|
||||
**如果求排列数就是外层 for 遍历背包,内层 for 循环遍历物品。**
|
||||
|
||||
- `dp[i]` 为从 0 ~ j 中选取排列,凑成 `i` 的排列数
|
||||
- `dp[i] += dp[i - nums[j]]`
|
||||
- `dp[0] = 1` 其它为 `0`
|
||||
- 都从前向后
|
||||
|
||||
### [70. 爬楼梯](https://leetcode.cn/problems/climbing-stairs/)
|
||||
|
||||
本题求的是排列数,因此外循环遍历背包容量,内循环遍历物品。
|
||||
|
||||
- `dp[i]` 为爬到第 `i` 阶的排列个数
|
||||
- `dp[i] += dp[i - nums[j]]`
|
||||
- `dp[0] = 1` 其它为 `0`
|
||||
- 都是从前往后
|
||||
|
||||
### [322. 零钱兑换](https://leetcode.cn/problems/coin-change/)
|
||||
|
||||
本题求的是组合数,因此外循环遍历物品,内循环遍历背包容量。
|
||||
|
||||
- `dp[j]` 为凑成金额 `j` 所需的最少硬币数
|
||||
- `dp[j] = min{dp[j - coins[i]] + 1, dp[j]}`
|
||||
- `dp[0] = 0` 其它为 `INT_MAX`
|
||||
- 都是从前往后
|
||||
|
||||
### [279.完全平方数](https://leetcode.cn/problems/perfect-squares/)
|
||||
|
||||
本题求的是组合数,因此外循环遍历物品,内循环遍历背包容量。
|
||||
|
||||
- `dp[j]` 为能凑成 `j` 的最少完全平方数的个数
|
||||
- `dp[j] = min{dp[j - i * i] + 1, dp[j]}`
|
||||
- `dp[0] = 0` 其它为 `INT_MAX`
|
||||
- 都是从前往后
|
||||
|
||||
## 多重背包
|
||||
|
||||
和 01 背包的区别在于,01 背包的每个元素只能用一次,而多重背包的每个物品能用 `ki` 次。
|
||||
|
||||
解决方法也很简单,把多重背包展开:
|
||||
|
||||
| | Weight | Value | Numbers |
|
||||
| :----: | :----: | :---: | :-----: |
|
||||
| Item 0 | 1 | 15 | 2 |
|
||||
| Item 1 | 3 | 20 | 3 |
|
||||
| Item 2 | 4 | 30 | 2 |
|
||||
|
||||
可以展开成这样的 01 背包:
|
||||
|
||||
| | Weight | Value |
|
||||
| :----: | :----: | :---: |
|
||||
| Item 0 | 1 | 15 |
|
||||
| Item 1 | 1 | 15 |
|
||||
| Item 2 | 3 | 20 |
|
||||
| Item 3 | 3 | 20 |
|
||||
| Item 4 | 3 | 20 |
|
||||
| Item 5 | 4 | 30 |
|
||||
| Item 6 | 4 | 30 |
|
||||
|
||||
```cpp
|
||||
void multi_knapsack_2d() {
|
||||
vector<int> weight = {1, 3, 4};
|
||||
vector<int> value = {15, 20, 30};
|
||||
vector<int> nums = {2, 3, 2};
|
||||
int knapsackWeight = 10;
|
||||
|
||||
// 展开
|
||||
for (int i = 0; i < nums.size(); i++) {
|
||||
while (nums[i] > 1) { // nums[i]保留到1,把其他物品都展开
|
||||
weight.push_back(weight[i]);
|
||||
value.push_back(value[i]);
|
||||
nums[i]--;
|
||||
}
|
||||
}
|
||||
|
||||
vector<int> dp(knapsackWeight + 1, 0);
|
||||
for (int i = 0; i < weight.size(); i++) { // 遍历物品
|
||||
for (int j = knapsackWeight; j >= weight[i]; j--) { // 遍历背包容量
|
||||
dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
|
||||
}
|
||||
}
|
||||
}
|
||||
```
|
||||
@@ -1,26 +0,0 @@
|
||||
# 总结
|
||||
|
||||
首先考虑递归 (e.g. s0206, s0024)
|
||||
|
||||
其次考虑双指针 (e.g. s0206, s0019, s0160)
|
||||
|
||||
递归遍历单链表:
|
||||
|
||||
```cpp
|
||||
void iter(ListNode *node) {
|
||||
// 终止条件
|
||||
if (node == nullptr) {
|
||||
return;
|
||||
}
|
||||
/*
|
||||
从前往后遍历
|
||||
*/
|
||||
iter(node->next);
|
||||
/*
|
||||
从后往前遍历
|
||||
*/
|
||||
return;
|
||||
}
|
||||
```
|
||||
|
||||
递归遍历的意义在于让回溯单链表,也就是先遍历到结尾,然后从后往前遍历到某个 condition 。
|
||||
@@ -1,40 +0,0 @@
|
||||
# 环形链表
|
||||
|
||||
[Leetcode](https://leetcode.com/problems/linked-list-cycle-ii/)
|
||||
|
||||
可以用回溯法解这道题。
|
||||
|
||||
首先递归遍历链表的一般结构如下:
|
||||
|
||||
```cpp
|
||||
void iter(ListNode *node) {
|
||||
// 终止条件
|
||||
if (node == nullptr) {
|
||||
return;
|
||||
}
|
||||
/*
|
||||
从前往后遍历
|
||||
*/
|
||||
iter(node->next);
|
||||
/*
|
||||
从后往前遍历
|
||||
*/
|
||||
return;
|
||||
}
|
||||
```
|
||||
|
||||
而查找链表中是否有环的思路是快慢指针,如果相遇则说明有环。
|
||||
|
||||
所以我们可以这样:
|
||||
|
||||
终止条件是快指针走到链表末尾或者快慢指针相遇。
|
||||
|
||||
从前往后遍历不需要做什么额外操作。
|
||||
|
||||
从后往前遍历的时候先把快指针的足迹记录到一个哈希表中,键值是节点地址,值是快指针经过的次数。
|
||||
|
||||
当出现以下两种情况的时候就说明找到了环的入口:
|
||||
|
||||
1. footprint[fast] == 1 && footprint[fast->next] > 1
|
||||
2. footprint[fast->next] == 1 && footprint[fast->next->next] > 1
|
||||
|
||||
@@ -1,128 +0,0 @@
|
||||
# LRU
|
||||
|
||||
[Leetcode 146. LRU Cache](https://leetcode.cn/problems/lru-cache/description/)
|
||||
|
||||
Header:
|
||||
|
||||
```cpp
|
||||
#ifndef S0146_LRU_CACHE_HPP
|
||||
#define S0146_LRU_CACHE_HPP
|
||||
|
||||
#include <cstdlib>
|
||||
#include <unordered_map>
|
||||
|
||||
class LRUCache {
|
||||
public:
|
||||
/**
|
||||
* @brief Least Recently Used Cache
|
||||
*
|
||||
* 这是一种常用的页面置换算法,选择最近最久未使用的页面予以淘汰
|
||||
*
|
||||
* @param capacity 容量,这是一个正整数
|
||||
*/
|
||||
LRUCache(int capacity);
|
||||
/**
|
||||
* @brief 读取数据
|
||||
*
|
||||
* @param key 数据对应的键值
|
||||
* @return 数据的值
|
||||
*/
|
||||
int get(int key);
|
||||
/**
|
||||
* @brief 放入对应的数据
|
||||
*
|
||||
* @param key 数据对应的键值
|
||||
* @param value 数据对应的值
|
||||
*/
|
||||
void put(int key, int value);
|
||||
|
||||
private:
|
||||
struct CacheNode {
|
||||
int key;
|
||||
int value;
|
||||
CacheNode *next;
|
||||
CacheNode *prev;
|
||||
CacheNode(int key, int value)
|
||||
: key(key), value(value), next(nullptr), prev(nullptr){};
|
||||
CacheNode(int key, int value, CacheNode *next, CacheNode *prev)
|
||||
: key(key), value(value), next(next), prev(prev){};
|
||||
};
|
||||
CacheNode *head;
|
||||
CacheNode *tail;
|
||||
int capacity;
|
||||
std::unordered_map<int, CacheNode *> map; // 键值是 key,值是该节点的指针
|
||||
void moveToHead(CacheNode *node); // 将节点移动到头部
|
||||
};
|
||||
|
||||
#endif
|
||||
```
|
||||
|
||||
Source:
|
||||
|
||||
```cpp
|
||||
#include "s0146_lru_cache.hpp"
|
||||
|
||||
void LRUCache::moveToHead(CacheNode *node) {
|
||||
// 如果是头部节点
|
||||
if (node == head) return;
|
||||
// 如果不是头部节点,但是是尾部节点
|
||||
if (node == tail) tail = node->prev;
|
||||
// 处理该节点的前后两个节点的指针
|
||||
if (node->prev) node->prev->next = node->next;
|
||||
if (node->next) node->next->prev = node->prev;
|
||||
// 将该节点移动到头部
|
||||
node->prev = nullptr;
|
||||
node->next = head;
|
||||
// 处理头部节点
|
||||
head->prev = node;
|
||||
head = node;
|
||||
}
|
||||
|
||||
LRUCache::LRUCache(int capacity) {
|
||||
this->capacity = capacity;
|
||||
head = nullptr;
|
||||
tail = nullptr;
|
||||
map = std::unordered_map<int, CacheNode *>();
|
||||
}
|
||||
|
||||
int LRUCache::get(int key) {
|
||||
if (map.size() == 0) return -1;
|
||||
if (map.count(key) == 0) return -1;
|
||||
moveToHead(map[key]);
|
||||
return map[key]->value;
|
||||
}
|
||||
|
||||
void LRUCache::put(int key, int value) {
|
||||
// 如果 key 已存在,则更新 value ,并将这个节点移动到头部
|
||||
if (map.count(key) == 1) {
|
||||
map[key]->value = value;
|
||||
moveToHead(map[key]);
|
||||
return;
|
||||
}
|
||||
// 否则创建该节点
|
||||
CacheNode *newNode = (CacheNode *)malloc(sizeof(CacheNode));
|
||||
newNode->value = value;
|
||||
newNode->key = key;
|
||||
newNode->next = head;
|
||||
newNode->prev = nullptr;
|
||||
// 处理头部节点
|
||||
if (head) head->prev = newNode;
|
||||
head = newNode;
|
||||
// 处理尾部节点
|
||||
if (map.size() == 0) tail = newNode;
|
||||
// 更新哈希表
|
||||
map[key] = newNode;
|
||||
// 如果容量已满
|
||||
if (map.size() > capacity) {
|
||||
// 更新尾部节点
|
||||
CacheNode *node = tail;
|
||||
if (tail->prev) {
|
||||
tail->prev->next = nullptr;
|
||||
tail = tail->prev;
|
||||
}
|
||||
// 移除该节点
|
||||
map.erase(node->key);
|
||||
free(node);
|
||||
}
|
||||
}
|
||||
```
|
||||
@@ -1,18 +0,0 @@
|
||||
# 合并两个有序链表
|
||||
|
||||
```cpp
|
||||
ListNode* mergeTwoLists(ListNode *a, ListNode *b) {
|
||||
if ((!a) || (!b)) return a ? a : b;
|
||||
ListNode head, *tail = &head, *aPtr = a, *bPtr = b;
|
||||
while (aPtr && bPtr) {
|
||||
if (aPtr->val < bPtr->val) {
|
||||
tail->next = aPtr; aPtr = aPtr->next;
|
||||
} else {
|
||||
tail->next = bPtr; bPtr = bPtr->next;
|
||||
}
|
||||
tail = tail->next;
|
||||
}
|
||||
tail->next = (aPtr ? aPtr : bPtr);
|
||||
return head.next;
|
||||
}
|
||||
```
|
||||
@@ -1,20 +0,0 @@
|
||||
# 长度最小的子数组
|
||||
|
||||
当题目中含有:
|
||||
|
||||
- 数组
|
||||
- 连续子数组
|
||||
|
||||
这两个关键词时,考虑使用非定长滑动窗口(即长度不固定的滑动窗口)
|
||||
|
||||
这种滑动窗口有两个关键:
|
||||
|
||||
- 起始指针,什么条件下移动
|
||||
- 终止指针,什么条件下移动
|
||||
|
||||
想清楚这两个问题就可以解答了。
|
||||
|
||||
## 相关题目
|
||||
|
||||
- [209. 长度最小的子数组](https://leetcode.com/problems/minimum-size-subarray-sum/)
|
||||
- [76. 最小覆盖子串](https://leetcode.com/problems/minimum-window-substring/)
|
||||
@@ -1,91 +0,0 @@
|
||||
# 排列问题
|
||||
|
||||
排列问题:N 个数按一定规则全排列,有几种排列方式
|
||||
|
||||
## [46. 全排列](https://leetcode.cn/problems/permutations/)
|
||||
|
||||
## [47. 全排列 II](https://leetcode.cn/problems/permutations-ii/)
|
||||
|
||||
和 s0046 相比就加了去重。有两种去重思路,一个是用哈希表记录每一层的使用情况,另一种是排序 + 判断,后者性能更好所以优先选择后者。
|
||||
|
||||
哈希表法:
|
||||
|
||||
```cpp
|
||||
#include "s0047_permutations_ii.hpp"
|
||||
|
||||
void permuteUniqueDFS(vector<int> &path, vector<vector<int>> &result,
|
||||
vector<bool> &used, vector<int> &nums) {
|
||||
int len = nums.size();
|
||||
// 终止条件
|
||||
if (path.size() == len) {
|
||||
result.push_back(path);
|
||||
return;
|
||||
}
|
||||
|
||||
// 创建一个哈希表用来记录当前层中使用过的元素
|
||||
unordered_map<int, bool> map;
|
||||
|
||||
// 开始迭代
|
||||
for (int i{0}; i < len; ++i) {
|
||||
// 如果当前元素在树枝或树层使用过,则跳过
|
||||
if (used[i] || map.count(nums[i]) == 1) continue;
|
||||
// 否则处理当前节点
|
||||
map[nums[i]] = true;
|
||||
path.push_back(nums[i]);
|
||||
used[i] = true;
|
||||
permuteUniqueDFS(path, result, used, nums);
|
||||
used[i] = false;
|
||||
path.pop_back();
|
||||
}
|
||||
}
|
||||
|
||||
vector<vector<int>> S0047::permuteUnique(vector<int> &nums) {
|
||||
vector<int> path{};
|
||||
vector<vector<int>> result{};
|
||||
vector<bool> used(nums.size(), false);
|
||||
permuteUniqueDFS(path, result, used, nums);
|
||||
return result;
|
||||
}
|
||||
```
|
||||
|
||||
排序 + 判断:
|
||||
|
||||
```cpp
|
||||
void permuteUniqueDFS(vector<int> &path, vector<vector<int>> &result,
|
||||
vector<bool> &used, vector<int> &nums, int startIndex) {
|
||||
int len = nums.size();
|
||||
// 终止条件
|
||||
if (path.size() == len) {
|
||||
result.push_back(path);
|
||||
return;
|
||||
}
|
||||
|
||||
// 开始迭代
|
||||
for (int i{0}; i < len; ++i) {
|
||||
// 如果当前元素在树层使用过,则跳过
|
||||
if (used[i] || (i > 0 && nums[i] == nums[i - 1] && used[i - 1] == false))
|
||||
continue;
|
||||
// 否则处理当前节点
|
||||
path.push_back(nums[i]);
|
||||
used[i] = true;
|
||||
permuteUniqueDFS(path, result, used, nums, i + 1);
|
||||
used[i] = false;
|
||||
path.pop_back();
|
||||
}
|
||||
}
|
||||
|
||||
vector<vector<int>> S0047::permuteUnique(vector<int> &nums) {
|
||||
vector<int> path{};
|
||||
vector<vector<int>> result{};
|
||||
vector<bool> used(nums.size(), false);
|
||||
sort(nums.begin(), nums.end());
|
||||
permuteUniqueDFS(path, result, used, nums, 0);
|
||||
return result;
|
||||
}
|
||||
```
|
||||
|
||||
## [332. 重新安排行程](https://leetcode.cn/problems/reconstruct-itinerary/)
|
||||
|
||||
这道题本来是想不到回溯法的,但是如果某道题能够拆分成多个步骤,每个步骤都在前一步的基础上进行选择,那么就可以用回溯法。
|
||||
|
||||

|
||||
@@ -1,11 +0,0 @@
|
||||
# 移除元素
|
||||
|
||||
查找数组中的目标元素 target ,原地移除该元素,返回移除后的数组长度。
|
||||
|
||||
双指针法,快指针用于查找新数组的元素,即不是 target 的元素,慢指针用于覆盖,即写入新数组的元素。
|
||||
|
||||
## 相关题目
|
||||
|
||||
- [27. 移除元素](https://leetcode.com/problems/remove-element/)
|
||||
- [24. 删除排序数组中的重复项](https://leetcode.com/problems/swap-nodes-in-pairs/)
|
||||
- [283. 移动零](https://leetcode.com/problems/move-zeroes/)
|
||||
@@ -1,23 +0,0 @@
|
||||
# 重复的子字符串
|
||||
|
||||
[459. Repeated Substring Pattern](https://leetcode.com/problems/repeated-substring-pattern/)
|
||||
|
||||
给定一个非空的字符串,判断它是否可以由它的一个子串重复多次构成。给定的字符串只含有小写英文字母,并且长度不超过10000。
|
||||
|
||||
示例:
|
||||
|
||||
输入: "abab"
|
||||
|
||||
输出: True
|
||||
|
||||
解释: 可由子字符串 "ab" 重复两次构成。
|
||||
|
||||
## 方法一
|
||||
|
||||
将两个 s 拼接在一起,如果里面还出现一个 s 的话,就认为是由重复字符串构成的。
|
||||
|
||||
## 方法二
|
||||
|
||||
假设 s 是由 n 个 x 构成的,那么它的最长公共前后缀的长度是 `(n - 1) * len(x)` 。
|
||||
|
||||
也就是说 `len(s) % (len(s) - (n - 1) * len(x)) == 0`
|
||||
@@ -1,7 +0,0 @@
|
||||
# 左旋转字符串
|
||||
|
||||
[Leetcode](https://leetcode.cn/problems/zuo-xuan-zhuan-zi-fu-chuan-lcof/)
|
||||
|
||||
涉及到字符串翻转/旋转,都可以考虑全剧翻转+局部翻转。
|
||||
|
||||
比如这道题就可以先翻转前半部分,再翻转后半部分,最后翻转整个字符串。
|
||||
@@ -1,27 +0,0 @@
|
||||
# 翻转字符串里的单词
|
||||
|
||||
[Leetcode](https://leetcode.com/problems/reverse-words-in-a-string/)
|
||||
|
||||
1. 去除单词中的额外空格
|
||||
2. 翻转整个字符串
|
||||
3. 挨个翻转单词
|
||||
|
||||
双指针去除额外空格:
|
||||
|
||||
如果快指针指向的是空格则跳过;
|
||||
|
||||
如果快指针指向的不是空格则把 `s[fast]` 覆盖到 `s[slow]`;
|
||||
|
||||
如果快指针指向的是空格并且下一个指向的不是空格,则在 `s[slow]` 处添加一个新空格(前提是 `slow` 不为 `0`,因为这种情况代表字符串的开头是空格)。
|
||||
|
||||
翻转字符串:
|
||||
|
||||
```cpp
|
||||
void reverseSubStr(string &s, int begin, int end) {
|
||||
for (; begin < end; ++begin, --end) {
|
||||
auto tmp = s[begin];
|
||||
s[begin] = s[end];
|
||||
s[end] = tmp;
|
||||
}
|
||||
}
|
||||
```
|
||||
@@ -1,190 +0,0 @@
|
||||
# 排序算法
|
||||
|
||||
在这里规定:
|
||||
|
||||
- 数组是 `arr[0...k]`
|
||||
- 排序是指从左到右从小到大排列
|
||||
- 有序区是指数组中的一个子数组(子数组要求连续,子序列不要求连续),该子数组已排好序
|
||||
- 无序区是指数组中的一个子数组,该子数组未排好序
|
||||
|
||||
## 插入排序
|
||||
|
||||
`arr[0...i]` 为有序区,`arr[i+1...k]` 为无序区,有序区长度一开始为 1。
|
||||
|
||||
每次排序将 `arr[i+1]` 插入到有序区中的合适位置。
|
||||
|
||||
插入到合适位置是指,插入进去后有序区后面部分的元素后移。
|
||||
|
||||
```cpp
|
||||
void insertSort(std::vector<int> &v) {
|
||||
int len = v.size();
|
||||
if (len == 1) return;
|
||||
|
||||
// 有序区 [0...i],无序区 [i+1...len-1]
|
||||
for (int i = 0; i < len - 1; ++i) {
|
||||
// 找到 v[i+1] 在有序区中的位置
|
||||
// 从后往前遍历有序区
|
||||
int j = i;
|
||||
while (v[i + 1] < v[j]) {
|
||||
--j;
|
||||
}
|
||||
// v[i+1] 应该插入到 v[j+1] 的位置
|
||||
// 先把原本的 v[j+1...i] 往后挪一位
|
||||
int tmp = v[i + 1];
|
||||
for (int x = i; j + 1 <= x; --x) {
|
||||
v[x + 1] = v[x];
|
||||
}
|
||||
// 插入 v[i+1]
|
||||
v[j + 1] = tmp;
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
时间复杂度:双重循环,所以为 **O(N^2)**
|
||||
|
||||
空间复杂度:占用内存随着排序总数 n 的增大而等比增大,所以为 **O(1)**
|
||||
|
||||
稳定性:不改变其它元素间的相对位置,所以**稳定**
|
||||
|
||||
## 冒泡排序
|
||||
|
||||
`arr[0...i]` 为无序区,`arr[i+1...k]` 为有序区,有序区长度一开始为 0。
|
||||
|
||||
每一次遍历无序区中的元素,将最大值放到无序区末尾。
|
||||
|
||||
具体是怎么放到末尾的呢?从后往前遍历无序区,比较相邻的两个元素,将大的那个元素往后挪。
|
||||
|
||||
```cpp
|
||||
void bubbleSort(std::vector<int> &v) {
|
||||
int len = v.size();
|
||||
if (len == 1) return;
|
||||
|
||||
// 无序区 [0...i],有序区 [i+1...len-1]
|
||||
for (int i = len - 1; i >= 0; --i) {
|
||||
// 从前往后遍历无序区
|
||||
for (int j = 0; j < i; ++j) {
|
||||
// 对比相邻的两个元素,把大的那个往后移
|
||||
if (v[j] > v[j + 1]) {
|
||||
v[j] = v[j] ^ v[j + 1];
|
||||
v[j + 1] = v[j] ^ v[j + 1];
|
||||
v[j] = v[j] ^ v[j + 1];
|
||||
}
|
||||
}
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
时间复杂度:双重循环,所以为 **O(N^2)**
|
||||
|
||||
空间复杂度:占用内存随着排序总数 n 的增大而等比增大,所以为 **O(1)**
|
||||
|
||||
稳定性:不改变其它元素间的相对位置,所以**稳定**
|
||||
|
||||
## 选择排序
|
||||
|
||||
`arr[0...i]` 为无序区,`arr[i+1...k]` 为有序区,有序区长度一开始为 0。
|
||||
|
||||
每一次遍历无序区中的元素,将最大值放到无序区末尾。
|
||||
|
||||
具体是怎么放到末尾的呢?从后往前遍历无序区,找到最大值的下标,然后将这个值和无序区末尾元素交换。
|
||||
|
||||
```cpp
|
||||
void selectionSort(std::vector<int> &v) {
|
||||
int len = v.size();
|
||||
if (len == 1) return;
|
||||
|
||||
int maxIndex = 0;
|
||||
int tmp = v[0];
|
||||
|
||||
// 无序区 [0...i],有序区 [i+1...len-1]
|
||||
for (int i = len - 1; i >= 0; --i) {
|
||||
maxIndex = 0;
|
||||
// 从前往后遍历无序区
|
||||
for (int j = 0; j <= i; ++j) {
|
||||
// 找到最大值的索引
|
||||
if (v[j] > v[maxIndex]) maxIndex = j;
|
||||
}
|
||||
// 交换最大值和无序区末尾元素
|
||||
tmp = v[i];
|
||||
v[i] = v[maxIndex];
|
||||
v[maxIndex] = tmp;
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
时间复杂度:双重循环,所以为 **O(N^2)**
|
||||
|
||||
空间复杂度:占用内存随着排序总数 n 的增大而等比增大,所以为 **O(1)**
|
||||
|
||||
稳定性:因为会与有序区末尾元素进行交换,改变了元素间的相对位置,所以**不稳定**
|
||||
|
||||
## 快速排序
|
||||
|
||||
选择一个“基准” (pivot),一般选择最左侧元素,比如 `pivot = arr[0]`。
|
||||
|
||||
现在我们要做的是,将比 `pivot` 小的元素放到它的左侧,将比它大的元素放在右侧,排序完后就成了这样:
|
||||
|
||||
`arr[0...x]`, `pivot`, `arr[y...k]`
|
||||
|
||||
其中 `arr[0...x]` 中的每一个元素都比 `pivot` 小,`arr[y...k]` 中的每个元素都比 `pivot` 大。
|
||||
|
||||
但是 `arr[0...x]` 和 `arr[y...k]` 是无序的,怎么办呢?
|
||||
|
||||
递归调用快排,对 `arr[0...x]` 和 `arr[y...k]` 排序。
|
||||
|
||||
```cpp
|
||||
void quickSort(std::vector<int> &v, int left, int right) {
|
||||
if (left >= right) return;
|
||||
int pivot = v[left];
|
||||
int tmp = 0;
|
||||
// 双指针
|
||||
// i = left 从左到右
|
||||
// j = right 从右到左
|
||||
int i = left;
|
||||
int j = right;
|
||||
while (i < j) {
|
||||
// 移动 j
|
||||
// 从右往左找到第一个比 pivot 小的 v[j]
|
||||
// 此时 v[j+1...k] 都比 pivot 大
|
||||
while (i < j && v[j] >= pivot) --j;
|
||||
// 把这个数覆盖到左侧 v[i]
|
||||
if (i < j) {
|
||||
v[i] = v[j];
|
||||
++i;
|
||||
}
|
||||
// 移动 i
|
||||
// 从左往右找到第一个比 pivot 大的 v[i]
|
||||
// 此时 v[0...i-1] 都比 pivot 小
|
||||
while (i < j && v[i] <= pivot) ++i;
|
||||
// 把这个数覆盖到右侧 v[j]
|
||||
if (i < j) {
|
||||
v[j] = v[i];
|
||||
--j;
|
||||
}
|
||||
}
|
||||
// 出循环后 i == j
|
||||
// 此时左侧和右侧都已经处理完毕
|
||||
// 接下来把 pivot 放到 v[i] 即可
|
||||
v[i] = pivot;
|
||||
// 递归处理左侧
|
||||
quickSort(v, left, i - 1);
|
||||
// 递归处理右侧
|
||||
quickSort(v, i + 1, right);
|
||||
}
|
||||
```
|
||||
|
||||
时间复杂度:最坏情况下为**O(N^2)**,平均时间复杂度为**O(N·logN)**
|
||||
|
||||
空间复杂度: 和时间复杂度相关,每次递归需要的空间是固定的,总体空间复杂度即为递归层数,因此平均/最好空间复杂度为 **O(logN)**,最坏空间复杂度为 **O(N)**
|
||||
|
||||
稳定性:**不稳定**
|
||||
|
||||
## 桶排序
|
||||
|
||||
[一看就懂的原理](https://www.cs.usfca.edu/~galles/visualization/BucketSort.html)
|
||||
|
||||
时间复杂度:取决于桶数量和数据分散程度,最好情况下可以达到**O(N)**,最坏情况下为**O(N^2)**,平均**O(N+K)**
|
||||
|
||||
空间复杂度:最坏**O(N·K)**
|
||||
|
||||
稳定性:**稳定**
|
||||
@@ -1,9 +0,0 @@
|
||||
# 切割问题
|
||||
|
||||
切割问题:一个字符串按一定规则有几种切割方式
|
||||
|
||||
## [131. 分割回文串](https://leetcode.cn/problems/palindrome-partitioning/)
|
||||
|
||||

|
||||
|
||||
## [93. 复原 IP 地址](https://leetcode.cn/problems/restore-ip-addresses/)
|
||||
@@ -1,160 +0,0 @@
|
||||
# 总结
|
||||
|
||||
## 栈
|
||||
|
||||
使用场景:
|
||||
|
||||
1. 需要先进后出的数据结构
|
||||
2. 匹配问题
|
||||
|
||||
经典题目:
|
||||
|
||||
[20. 有效的括号](https://leetcode.cn/problems/valid-parentheses/)
|
||||
|
||||
[1047. 删除字符串中的所有相邻重复项](https://leetcode.cn/problems/remove-all-adjacent-duplicates-in-string/)
|
||||
|
||||
### 变体:单调栈
|
||||
|
||||
栈中的元素单调递增或单调递减。
|
||||
|
||||
使用场景:通常是一维数组,要寻找任一个元素的右边或者左边第一个比自己大或者小的元素的位置。
|
||||
|
||||
拿找右边第一个比自己大的元素举例:
|
||||
|
||||
栈中存储元素的下标 i,比较栈顶元素 arr[i] 和当前元素 arr[j] 的大小,
|
||||
|
||||
如果栈顶元素 < 当前元素,那么 j - i 就是答案,栈顶元素出栈(注意是循环出栈,直到栈顶元素 > 当前元素);
|
||||
|
||||
如果栈顶元素 > 当前元素,则当前元素入栈。
|
||||
|
||||
时间复杂度:O(n)
|
||||
|
||||
经典题目:
|
||||
|
||||
[739. 每日温度](https://leetcode.com/problems/daily-temperatures/)
|
||||
|
||||
[496. 下一个更大元素 I](https://leetcode.com/problems/next-greater-element-i/)
|
||||
|
||||
[503. 下一个更大元素 II](https://leetcode.com/problems/next-greater-element-ii/)
|
||||
|
||||
Tips: 循环数组的处理方法:
|
||||
|
||||
```cpp
|
||||
for (int i{0}; i < 2 * len; ++i) {
|
||||
nums[i % len] ...
|
||||
}
|
||||
```
|
||||
|
||||
## 队列
|
||||
|
||||
使用场景:
|
||||
|
||||
1. 先进先出的数据结构
|
||||
2. 滑动窗口最值问题
|
||||
|
||||
### 变体:优先级队列
|
||||
|
||||
队列中的数据以 `<priority, value>` 的形式存储,每一个 `value` 都有一个 `priority` 。
|
||||
|
||||
当入队,我们根据 `priority` 将元素插入到队列的相应位置,队列中的元素总是按优先级升序或者降序排列。
|
||||
|
||||
```cpp
|
||||
#include <iostream>
|
||||
#include <queue>
|
||||
#include <string>
|
||||
#include <utility>
|
||||
|
||||
int main(int argc, const char *argv[]) {
|
||||
// priority 为 int 类型,value 为 std::string 类型
|
||||
std::priority_queue<std::pair<int, std::string>> q;
|
||||
// 写入元素
|
||||
q.push(std::make_pair(3, "Microsoft"));
|
||||
q.push(std::make_pair(1, "Surface"));
|
||||
q.push(std::make_pair(2, "Apple"));
|
||||
q.push(std::make_pair(4, "MacBook"));
|
||||
// 访问顶部元素
|
||||
std::cout << q.top().first << q.top().second << std::endl;
|
||||
// 删除顶部元素
|
||||
q.pop();
|
||||
// 检查是否为空
|
||||
if (q.empty()) {
|
||||
std::cout << "Empty" << std::endl;
|
||||
} else {
|
||||
std::cout << "Not empty" << std::endl;
|
||||
}
|
||||
return 0;
|
||||
}
|
||||
```
|
||||
|
||||
输出:
|
||||
|
||||
```text
|
||||
4MacBook
|
||||
Not empty
|
||||
```
|
||||
|
||||
优先队列用一般用堆来实现,具有 `O(log n)` 时间复杂度的插入元素性能,`O(n)` 的初始化构造的时间复杂度。
|
||||
|
||||
经典题目:[239. 滑动窗口最大值](https://leetcode.cn/problems/sliding-window-maximum/)
|
||||
|
||||
奇技淫巧:随机删除元素
|
||||
|
||||
现在我们想以 `O(logn)` 的时间复杂度来删除元素,应该怎么做呢?
|
||||
|
||||
思路很简单,维护另一个优先队列——删除队列。
|
||||
|
||||
当我们要删除一个元素时,我们并不真的在原队列中删除它,而是把它放到删除队列中;
|
||||
|
||||
当我们要访问原队列栈顶时,看看原队列栈顶是不是等于删除队列栈顶,如果是,则循环删除原队列和删除队列的栈顶,直到栈顶不想等或者为空。
|
||||
|
||||
为什么这样做一定是正确的呢?有没有可能我们想要删除 x ,原队列栈顶也是 x ,而删除队列栈顶是 y ( y >= x ) 呢?
|
||||
|
||||
这是不可能的,因为如果 y >= x ,那么原队列栈顶就不可能是 x 。
|
||||
|
||||
### 变体:单调队列
|
||||
|
||||
优先队列有另外一个名字:二叉堆,它的数据结构本质上并不是队列,时间复杂度不是线性的。
|
||||
|
||||
是否有线性复杂度的数据结构呢?
|
||||
|
||||
有,这就是单调队列。
|
||||
|
||||
单调队列的特性如下:
|
||||
|
||||
1. 它的数据结构本质依然是队列,因此具有线性时间复杂度
|
||||
2. 它并不能保证你弹出一个元素后,这个元素就真的在队列里删除了,也有可能当你在插入元素时会删掉队列里的其它元素
|
||||
3. 它能保证的是,队列中所有元素单调(递减),队首元素一定是队列里的最值。
|
||||
|
||||
经典题目:[239. 滑动窗口最大值](https://leetcode.cn/problems/sliding-window-maximum/)
|
||||
|
||||
我们看看这道题里的单调队列是怎么实现的。这里我们采用 `deque` ,相比于 `queue` ,它能同时对队首和队尾进行操作。
|
||||
|
||||
```cpp
|
||||
#include <deque>
|
||||
|
||||
class MyQueue {
|
||||
public:
|
||||
std::deque<int> que;
|
||||
|
||||
void pop(int value) {
|
||||
// 只有当要弹出的元素等于队首时,才会弹出
|
||||
// 这样做没问题吗?
|
||||
// 没问题,因为我们只关注队首元素是不是最大的,只要我们想弹出的元素不是队首元素,那就可以不用管
|
||||
if (value == que.front() && !que.empty()) {
|
||||
que.pop_front();
|
||||
}
|
||||
}
|
||||
|
||||
void push(int value) {
|
||||
// 当我们要插入的元素比队尾元素大时,就一直弹出队尾元素,直到小于等于队尾元素为止
|
||||
// 这样做没问题吗?
|
||||
// 没问题,因为我们只关注队首元素是不是最大的,其它元素要不要都无所谓。
|
||||
while (value > que.back() && !que.empty()) {
|
||||
que.pop_back();
|
||||
}
|
||||
que.push_back(value);
|
||||
}
|
||||
|
||||
int front(void) { return que.front(); }
|
||||
};
|
||||
```
|
||||
@@ -1,13 +0,0 @@
|
||||
# 总结
|
||||
|
||||
以下底层实现为二叉搜索树,增删操作时间复杂度是 log(n):
|
||||
|
||||
- `map`
|
||||
- `set`
|
||||
- `multimap`
|
||||
- `multiset`
|
||||
|
||||
以下底层实现是哈希表,增删操作时间复杂度是 log(1):
|
||||
|
||||
- `unordered_map`
|
||||
- `unordered_set`
|
||||
@@ -1,44 +0,0 @@
|
||||
# 哈希表
|
||||
|
||||
```cpp
|
||||
#include <iostream>
|
||||
#include <string>
|
||||
#include <unordered_map>
|
||||
|
||||
int main(int argc, const char *argv[]) {
|
||||
// key 为 std::string 类型的,value 为 int 类型的
|
||||
std::unordered_map<std::string, int> map;
|
||||
// 插入
|
||||
map["foo"] = 1;
|
||||
map["bar"] = 2;
|
||||
map["non"] = 3;
|
||||
// 访问
|
||||
std::cout << map["foo"] << std::endl;
|
||||
// 删除
|
||||
map.erase("foo");
|
||||
// 判断元素是否存在
|
||||
if (map.count("bar") > 0) {
|
||||
std::cout << "Exist" << std::endl;
|
||||
} else {
|
||||
std::cout << "Not exist" << std::endl;
|
||||
}
|
||||
// 另一种判断元素是否存在的方法
|
||||
// find() 会返回元素的正向迭代器,如果没找到则返回 end()
|
||||
if (map.find("bar") != map.end()) {
|
||||
std::cout << "Exist" << std::endl;
|
||||
} else {
|
||||
std::cout << "Not exist" << std::endl;
|
||||
}
|
||||
// 合并两个 unordered_map
|
||||
std::unordered_map<std::string, int> newMap;
|
||||
newMap["microsoft"] = 1;
|
||||
newMap["surface"] = 1;
|
||||
map.insert(newMap.begin(), newMap.end());
|
||||
// 遍历
|
||||
for (std::unordered_map<std::string, int>::iterator iter = map.begin();
|
||||
iter != map.end(); ++iter) {
|
||||
std::cout << iter->first << iter->second << std::endl;
|
||||
}
|
||||
return 0;
|
||||
}
|
||||
```
|
||||
@@ -1,44 +0,0 @@
|
||||
# 排序
|
||||
|
||||
升序排序:
|
||||
|
||||
```cpp
|
||||
void ascending(std::vector<int> &x) {
|
||||
// #include <algorithm>
|
||||
std::sort(x.begin(), x.end());
|
||||
}
|
||||
```
|
||||
|
||||
降序排序:
|
||||
|
||||
```cpp
|
||||
void descending(std::vector<int> &x) {
|
||||
// #include <algorithm>
|
||||
// #include <functional>
|
||||
std::sort(x.begin(), x.end(), std::greater<int>());
|
||||
}
|
||||
```
|
||||
|
||||
自定义比较函数:
|
||||
|
||||
```cpp
|
||||
struct Data {
|
||||
std::string name;
|
||||
int age;
|
||||
};
|
||||
|
||||
/**
|
||||
* @brief 自定义比较函数
|
||||
*
|
||||
* @param a 第一个待比较的值
|
||||
* @param b 第二个待比较的值
|
||||
* @return 返回为 true 时代表 a 应该放在 b 前面
|
||||
*/
|
||||
bool compareFunc(Data &a, Data &b) {
|
||||
return a.name.length() > b.name.length();
|
||||
}
|
||||
|
||||
void customCompare(std::vector<Data> &x) {
|
||||
std::sort(x.begin(), x.end(), compareFunc);
|
||||
}
|
||||
```
|
||||
@@ -1,57 +0,0 @@
|
||||
# 字符串
|
||||
|
||||
```cpp
|
||||
#include <iostream>
|
||||
#include <string>
|
||||
|
||||
int main(int argc, const char *argv[]) {
|
||||
// 输出到 stdout
|
||||
std::cout << "Input your string: ";
|
||||
// 从 stdin 读取
|
||||
std::string input;
|
||||
// 不能读入空格,以空格、制表符、回车符作为结束标志
|
||||
std::cin >> input;
|
||||
// 可以读入空格和制表符,以回车符作为结束标志
|
||||
std::getline(std::cin, input);
|
||||
|
||||
// 创建一个字符串
|
||||
std::string str1 = "surface";
|
||||
// 深拷贝一个字符串
|
||||
std::string str2 = str1;
|
||||
std::string str3 = std::string(str1);
|
||||
// 从下标 1 开始深拷贝
|
||||
std::string str4 = std::string(str1, 1);
|
||||
// 从下标 1 开始深拷贝,长度为 2
|
||||
std::string str5 = std::string(str1, 1, 2);
|
||||
std::string str6 = str1.substr(1, 2);
|
||||
|
||||
// 长度
|
||||
int len = str1.length();
|
||||
// 是否为空
|
||||
bool isEmpty = str1.empty();
|
||||
// 类型转换
|
||||
int val = std::stoi("1024");
|
||||
|
||||
// 读取
|
||||
std::cout << str1[0] << std::endl;
|
||||
std::cout << str1.front() << std::endl;
|
||||
std::cout << str1.back() << std::endl;
|
||||
// 在结尾追加
|
||||
str1.append(" book");
|
||||
// 在索引为 6 的字符前面插入字符串
|
||||
str1.insert(6, "foo");
|
||||
// 替换从 0 开始,长度为 2 的子字符串
|
||||
str1.replace(0, 2, "msft");
|
||||
// 删除从 0 开始,长度为 4 的子字符串
|
||||
str1.erase(0, 4);
|
||||
|
||||
// 两个字符串组合
|
||||
std::string str7 = str1 + str2;
|
||||
// 两个字符串比较
|
||||
bool isEqual = str1 == str2;
|
||||
// 寻找子字符串出现的起始位置
|
||||
int startIndex = str1.find("foo");
|
||||
// 从索引 2 开始往后搜索
|
||||
startIndex = str1.find("foo", 2);
|
||||
}
|
||||
```
|
||||
@@ -1,59 +0,0 @@
|
||||
# 向量
|
||||
|
||||
```cpp
|
||||
#include <algorithm>
|
||||
#include <iostream>
|
||||
#include <vector>
|
||||
|
||||
int main(int argc, const char *argv[]) {
|
||||
// 初始化
|
||||
std::vector<int> v1;
|
||||
// 创建长度为 10 的向量(缺省值填充)
|
||||
std::vector<int> v2(10);
|
||||
// 创建长度为 10,值为 7 的向量
|
||||
std::vector<int> v3(10, 7);
|
||||
// 从另一个向量深拷贝
|
||||
std::vector<int> v4 = v2;
|
||||
|
||||
// 释放内存
|
||||
v4.clear();
|
||||
v4.shrink_to_fit();
|
||||
|
||||
// 修改数据
|
||||
v3[1] = 100;
|
||||
// 删除数据,传递进去的参数是迭代器
|
||||
v3.erase(v3.begin() + 1);
|
||||
v3.erase(v3.begin() + 3, v3.end());
|
||||
// 插入到尾部
|
||||
v3.push_back(67);
|
||||
// 弹出尾部元素
|
||||
v3.pop_back();
|
||||
// 插入到最前面和最后面
|
||||
// 意思是插入完成后,第一个参数所在位置的值是第二个参数
|
||||
v3.insert(v3.begin(), 2);
|
||||
v3.insert(v3.end(), 2);
|
||||
// 访问第一个数和最后一个数
|
||||
std::cout << v3.front() << " " << v3.back() << std::endl;
|
||||
// 合并两个向量
|
||||
// 意思是把 v2 向量插入到 v3 的尾部
|
||||
v3.insert(v3.end(), v2.begin(), v2.end());
|
||||
|
||||
// 交换 v3 和 v2,相当于把 v3 的内容覆盖到 v2,把 v2 的内容覆盖到 v3
|
||||
v3.swap(v2);
|
||||
// 重新调整大小
|
||||
// 如果传入的参数超过了向量原本的长度,则在扩展后的末尾填充缺省值
|
||||
// 如果传入的参数小于向量原本的长度,则只保留前 N 个元素,后面的部分删掉
|
||||
v3.resize(10);
|
||||
// 如果传入的参数超过了向量原本的长度,则在扩展后的末尾填充 99
|
||||
v3.resize(15, 99);
|
||||
// 查找最大值和最小值,返回的是一个指针
|
||||
// #include <algorithm>
|
||||
std::cout << *std::max_element(v3.begin(), v3.end()) << std::endl;
|
||||
std::cout << *std::min_element(v3.begin(), v3.end()) << std::endl;
|
||||
|
||||
for (int i = 0; i < v3.size(); ++i) {
|
||||
std::cout << v3[i] << " ";
|
||||
}
|
||||
std::cout << std::endl;
|
||||
}
|
||||
```
|
||||
@@ -1,33 +0,0 @@
|
||||
# 股票问题
|
||||
|
||||
## [122. 买卖股票的最佳时机 II](https://leetcode.cn/problems/best-time-to-buy-and-sell-stock-ii/)
|
||||
|
||||
- `dp[i][0]` 表示第 i 天持有股票情况下的资产总额,`dp[i][1]` 表示第 i 天没有持有股票情况下的资产总额。这里的资产不包括股票本身的价值,只包括自身的现金,如果你在第 1 天买入了股票,那么你的资产总额是 `-prices[0]`。
|
||||
- 递推公式:
|
||||
- 我们先来讨论 `dp[i][0]`,也就是第 i 天持有股票时的资产,分两种情况
|
||||
- 第 i - 1 天持有股票,那么第 i 天的资产就是 `dp[i - 1][0]`
|
||||
- 第 i - 1 天没持有股票,那么第 i 天的资产就是 `dp[i - 1][1] - prices[i]`
|
||||
- 取这两者的最大值即为第 i 天的最大资产 `dp[i][0] = max(dp[i - 1][0], dp[i - 1][1] - prices[i])`
|
||||
- 同理 `dp[i][1]` 也分两种情况
|
||||
- 第 i - 1 天持有股票,那么第 i 天的资产就是 `dp[i - 1][0] + prices[0]`
|
||||
- 第 i - 1 天没持有股票,那么第 i 天的资产就是 `dp[i - 1][1]`
|
||||
- 取这两者的最大值即为第 i 天的最大资产 `dp[i][1] = max(dp[i - 1][0] + prices[i], dp[i - 1][1])`
|
||||
- 初始化
|
||||
- `dp[0][0] = -prices[0]`
|
||||
- `dp[0][1] = 0`
|
||||
- 遍历顺序:从前往后
|
||||
|
||||
## [123.买卖股票的最佳时机III](https://leetcode.cn/problems/best-time-to-buy-and-sell-stock-iii/)
|
||||
|
||||
- `dp[i][j][k]` 是第 `i` 笔交易中,第 `j` 天,是否持有股票时的总资产
|
||||
- 递推公式:
|
||||
- `dp[0][i][0] = max(dp[0][i - 1][0], -prices[i])`
|
||||
- `dp[0][i][1] = max(dp[0][i - 1][1], dp[0][i][0] + prices[i])`
|
||||
- `dp[1][i][0] = max(dp[1][i - 1][0], dp[0][i - 1][1] - prices[i])`
|
||||
- `dp[1][i][1] = max(dp[1][i - 1][1], dp[0][i - 1][0] + prices[i])`
|
||||
- 初始化:
|
||||
- `dp[i][0][0] = -prices[0]`
|
||||
- `dp[i][0][1] = 0`
|
||||
- 遍历顺序:
|
||||
- 先遍历 `i`
|
||||
- 再遍历 `j` 和 `k`
|
||||
@@ -1,7 +0,0 @@
|
||||
# 总结
|
||||
|
||||
字符串局部翻转/旋转考虑先全局翻转,再局部翻转。
|
||||
|
||||
字符串原地插入/替换新字符,先扩展字符串的长度,然后双指针从后往前,按条件覆盖到慢指针。
|
||||
|
||||
Pattern 匹配考虑 KMP 算法。
|
||||
@@ -1,126 +0,0 @@
|
||||
# 子序列问题
|
||||
|
||||
子序列问题一般涉及到两个序列 `s` 和 `t`,`dp[i][j]` 一般设计成 `i` 和 `j` 为这两个序列的索引。
|
||||
|
||||
我们需要讨论的是当 `s[i] == t[j]` 和 `s[i] != t[j]` 时,如何由以下三个推导出 `dp[i][j]`:
|
||||
|
||||
1. `dp[i - 1][j - 1]`
|
||||
2. `dp[i - 1][j]`
|
||||
3. `dp[i][j - 1]`
|
||||
|
||||
## [300. 最长递增子序列](https://leetcode.cn/problems/longest-increasing-subsequence/)
|
||||
|
||||
- `dp[i]` 表示以 `nums[i]` 结尾的最长递增子序列的长度
|
||||
- 遍历 `j` 从 `0` 到 `i`, `if (nums[i] > nums[j]) dp[i] = max(dp[i], dp[j] + 1)`
|
||||
- `dp[i] = 1`
|
||||
- 外层遍历 `i` 内层遍历 `j`,都是从前往后
|
||||
|
||||
## [674. 最长连续递增序列](https://leetcode.cn/problems/longest-continuous-increasing-subsequence/)
|
||||
|
||||
- `dp[i]` 表示以 `nums[i]` 结尾的最长连续递增子序列的长度
|
||||
- 递推公式:
|
||||
- `if (nums[i] > nums[i - 1]) dp[i] = dp[i - 1] + 1`
|
||||
- `if (nums[i] <= nums[i - 1]) dp[i] = 1`
|
||||
- `dp[0] = 1`
|
||||
- 从前往后
|
||||
|
||||
## [718. 最长重复子数组](https://leetcode.cn/problems/maximum-length-of-repeated-subarray/)
|
||||
|
||||
- `dp[i][j]` 表示以 `i` 为下标结尾的 A 和以 `j` 为下标结尾的 B 的最长重复子数组
|
||||
- `if (nums1[i] == nums2[j]) dp[i][j] = dp[i - 1][j - 1] + 1` 否则为 `0`
|
||||
- 初始化:
|
||||
- `if (nums1[i] == nums2[0]) dp[i][0] = 1` 否则为 `0`
|
||||
- `if (nums1[0] == nums2[j]) dp[0][j] = 1` 否则为 `0`
|
||||
- 其它都初始化为 `0`
|
||||
- 都从前往后遍历,下标从 `1` 开始
|
||||
|
||||
## [1143. 最长公共子序列](https://leetcode.cn/problems/longest-common-subsequence/)
|
||||
|
||||
- `dp[i][j]` 表示以 `i` 为下标结尾的 text1 和以 `j` 为下标结尾的 text2 的最长公共子序列
|
||||
- 递推公式
|
||||
- `if (text1[i] == text2[j]) dp[i][j] = dp[i - 1][j - 1] + 1`
|
||||
- `if (text1[i] != text2[j]) dp[i][j] = max(dp[i - 1][j], dp[i][j - 1])`
|
||||
- 只需要初始化三个:
|
||||
- `dp[0][0]`
|
||||
- `dp[1][0]`
|
||||
- `dp[0][1]`
|
||||
|
||||
## [53. 最大子序和](https://leetcode.cn/problems/maximum-subarray/)
|
||||
|
||||
- `dp[i]` 为包括下标 `i` 的最大连续子序列和
|
||||
- `max(dp[i - 1] + nums[i], nums[i])`
|
||||
- `dp[0] = nums[0]`
|
||||
- 从前往后
|
||||
|
||||
## [115. 不同的子序列](https://leetcode.cn/problems/distinct-subsequences/)
|
||||
|
||||
- `dp[i][j]` 表示在 `s[...i]` 中 `t[...j]` 出现的的次数
|
||||
- 递推公式:
|
||||
- `if (s[i] == t[j])`
|
||||
- 第一种组合方式是在 `s[...i-1]` 中 `t[...j-1]` 出现了 `dp[i - 1][j - 1]` 次,这时候我们把末尾的 `s[i]` 和 `t[j]` 分别加上去,之前的每一次匹配依然有效,所以出现次数为 `dp[i - 1][j - 1]`
|
||||
- 第二种组合方式是,`t[...j]` 有可能本身就在 `s[...i-1]` 中出现过,出现的次数是 `dp[i - 1][j]`
|
||||
- 把这两种情况的数量加起来就是 `dp[i][j]` 了:`dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j]`
|
||||
- `if (s[i] != t[j])`
|
||||
- 只有一种可能,那就是 `t[...j]` 本身就在 `s[...i-1]` 中出现过,出现次数为 `dp[i - 1][j]`
|
||||
- 需要初始化两个:
|
||||
- `dp[i][0]`
|
||||
- `dp[0][j]`
|
||||
- 都从前往后遍历
|
||||
|
||||
## [583. 两个字符串的删除操作](https://leetcode.cn/problems/delete-operation-for-two-strings/)
|
||||
|
||||
- `dp[i][j]` 表示 `word1[...i]` 和 `word2[...j]` 所需的操作数
|
||||
- 递推公式:
|
||||
- `if (word1[i] == word2[j]) dp[i][j] = dp[i - 1][j - 1]`
|
||||
- `if (word1[i] == word2[j]) dp[i][j] = min(dp[i - 1][j] + 1, dp[i][j - 1] + 1)`
|
||||
- 初始化
|
||||
- `dp[i][0] = i`
|
||||
- `dp[0][j] = j`
|
||||
- 从前往后遍历
|
||||
|
||||
## [72. 编辑距离](https://leetcode.cn/problems/edit-distance/)
|
||||
|
||||
- `dp[i][j]` 是把 `word1[...i]` 转换成 `word2[...j]` 所需的最少操作数
|
||||
- 递推公式:
|
||||
- `if (word1[i] == word2[j]) dp[i][j] = dp[i - 1][j - 1]`
|
||||
- `if (word1[i] != word2[j])`
|
||||
- 从 `dp[i - 1][j - 1]` 转换过去,需要把 `word1[i]` 替换成 `word2[j]`,也就是 `dp[i - 1][j - 1] + 1` 步操作
|
||||
- 从 `dp[i][j - 1]` 转换过去,需要在 `word1[...i]` 的末尾插入一个 `word2[j]`,也就是 `dp[i][j - 1] + 1` 步操作
|
||||
- 从 `dp[i - 1][j]` 转换过去,需要删除 `word1[i]`,也就是 `dp[i - 1][j] + 1` 步操作
|
||||
- 这三种情况取最小,即 `min(dp[i - 1][j - 1] + 1, dp[i][j - 1] + 1, dp[i - 1][j] + 1)`
|
||||
- 初始化:
|
||||
- `dp[i][0]`
|
||||
- `dp[0][j]`
|
||||
- 从前向后遍历
|
||||
|
||||
## [647. 回文子串](https://leetcode.cn/problems/palindromic-substrings/)
|
||||
|
||||
- `dp[i][j]` 表示 `s[i...j]` 是否是回文串
|
||||
- 递推公式:
|
||||
- `if (s[i] == s[j])`
|
||||
- `if (i == j) dp[i][j] = true`
|
||||
- `else if (j = i + 1) dp[i][j] = true`
|
||||
- `else dp[i][j] = dp[i + 1][j - 1]`
|
||||
- `if (s[i] != s[j]) dp[i][j] = false`
|
||||
- 全部初始化为 `false`
|
||||
- 遍历顺序:
|
||||
- `i` 从后往前,范围是 `0...len-1`
|
||||
- `j` 从前往后,范围是 `i...len-1`
|
||||
|
||||
## [516. 最长回文子序列](https://leetcode.cn/problems/longest-palindromic-subsequence/)
|
||||
|
||||
字串要连续,子序列不用连续。
|
||||
|
||||
- `dp[i][j]` 表示 `s[i...j]` 的最长回文子序列的长度
|
||||
- 递推公式:
|
||||
- `if (s[i] != s[j])`
|
||||
- `if (j = i + 1) dp[i][j] = 0`
|
||||
- `else dp[i][j] = dp[i + 1][j - 1]`
|
||||
- `if (s[i] == s[j])`
|
||||
- `if (i == j) dp[i][j] = 1`
|
||||
- `else if (j = i + 1) dp[i][j] = 2`
|
||||
- `else dp[i][j] = dp[i + 1][j - 1] + 2`
|
||||
- 全部初始化为 `0`
|
||||
- 遍历顺序:
|
||||
- `i` 从后往前,范围是 `0...len-1`
|
||||
- `j` 从前往后,范围是 `i...len-1`
|
||||
@@ -1,46 +0,0 @@
|
||||
# 子集问题
|
||||
|
||||
子集问题:一个 N 个数的集合里有多少符合条件的子集
|
||||
|
||||
## [78. 子集](https://leetcode.cn/problems/subsets/)
|
||||
|
||||
其实和切割问题非常像。
|
||||
|
||||
## [90. 子集 II](https://leetcode.cn/problems/subsets-ii/)
|
||||
|
||||
就是在 s0078 的基础上加了去重逻辑,和组合问题中的去重逻辑一样。
|
||||
|
||||
## [491. 递增子序列](https://leetcode.cn/problems/non-decreasing-subsequences/)
|
||||
|
||||
也是要去重,但是不能通过排序去重,因为排序之后顺序就全部打乱了。
|
||||
|
||||
这个去重同样要保留树枝重复,但去除树层重复。
|
||||
|
||||
思路很简单,每一层遍历的时候创建一个哈希表,用来记录当前元素是否遍历过,如果遍历过则跳过。
|
||||
|
||||
```cpp
|
||||
void findSubsequencesDFS(vector<int> &subsequences, vector<vector<int>> &result,
|
||||
vector<int> &nums, int startIndex) {
|
||||
int size = nums.size();
|
||||
// 结束条件
|
||||
if (startIndex == size) return;
|
||||
|
||||
// 初始化一个哈希表用来存储元素是否在数层中使用过
|
||||
unordered_map<int, bool> used;
|
||||
|
||||
for (int i = startIndex; i < size; ++i) {
|
||||
// 剪枝,如果元素在数层中使用过则跳过
|
||||
if (used.count(nums[i]) == 1) continue;
|
||||
// 当当前元素大于等于起始元素之前的元素时,将它添加进去
|
||||
if (startIndex == 0 || nums[i] >= nums[startIndex - 1]) {
|
||||
subsequences.push_back(nums[i]);
|
||||
if (subsequences.size() > 1) result.push_back(subsequences);
|
||||
used[nums[i]] = true;
|
||||
findSubsequencesDFS(subsequences, result, nums, i + 1);
|
||||
subsequences.pop_back();
|
||||
}
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
这种去重逻辑相比于之前的去重逻辑起始开销更大,因为每一层遍历都要创建一个新的哈希表,而之前的去重逻辑每一层遍历都用的是之前创建的向量。
|
||||
@@ -1,15 +0,0 @@
|
||||
# 替换空格
|
||||
|
||||
[Leetcode](https://leetcode.cn/problems/ti-huan-kong-ge-lcof/)
|
||||
|
||||
请实现一个函数,把字符串 s 中的每个空格替换成"%20"。
|
||||
|
||||
示例 1:
|
||||
|
||||
> 输入:s = "We are happy."
|
||||
>
|
||||
> 输出:"We%20are%20happy."
|
||||
|
||||

|
||||
|
||||
对于很多数组填充类问题,都可以先计算出扩展后数组的长度,然后从后往前双指针。
|
||||
@@ -1,32 +0,0 @@
|
||||
# 三数相加
|
||||
|
||||
[Leetcode 15. 3Sum](https://leetcode.com/problems/3sum/)
|
||||
|
||||
这是一道典型的双指针 + 排序的题目。
|
||||
|
||||
如果暴力枚举的话时间复杂度是 O(n^3) ,我们考虑用双指针来遍历。
|
||||
|
||||
双指针可以将 O(n^2) 的时间复杂度降到 O(n),如果这道题用了双指针的话可以将时间复杂度降到 O(n^2) 。
|
||||
|
||||
思路很简单,首先对数组从小到大排序,然后 `for i from 0 to end` ,这是第一重循环
|
||||
|
||||
然后在 [i+1, end] 这个区间里,定义一个 left 从左往右,和一个 right 从右往左。
|
||||
|
||||
终止条件是它们相遇,或者三数相加满足题目条件。
|
||||
|
||||
当三数之和小于 0 时,left 往右移;
|
||||
|
||||
当三数之和大于 0 时,right 往左移。
|
||||
|
||||
---
|
||||
|
||||
[Leetcode 18. 4Sum](https://leetcode.com/problems/4sum/)
|
||||
|
||||
和三数相加差不多,只不过我们把 `for i from 0 to end` 这个循环改成了双重循环
|
||||
|
||||
```text
|
||||
for i from 0 to end
|
||||
for j from i+1 to end
|
||||
```
|
||||
|
||||
其它都一样。时间复杂度 O(n^3)
|
||||
Reference in New Issue
Block a user