This commit is contained in:
@@ -32,8 +32,15 @@
|
||||
- [总结](./stack_and_queue.md)
|
||||
- [用栈实现队列 && 用队列实现栈](./impl_stack_queue.md)
|
||||
|
||||
# 二叉树
|
||||
|
||||
- [理论基础](./btree_basic.md)
|
||||
- [遍历](./btree_iter.md)
|
||||
|
||||
# STL
|
||||
|
||||
- [总结](./stl.md)
|
||||
|
||||
# 经典代码
|
||||
|
||||
- [合并两个有序链表](./merge_two_sorted_linked_lists.md)
|
||||
- [深度优先遍历](./dfs.md)
|
||||
- [广度优先遍历](./bfs.md)
|
||||
|
||||
@@ -1,36 +0,0 @@
|
||||
# 广度优先遍历
|
||||
|
||||
1. 保留全部节点状态,占用空间大
|
||||
2. 无回溯操作(即无入栈、出栈操作),运行速度快
|
||||
3. 对于解决最短或最少问题特别有效,而且寻找深度小(每个结点只访问一遍,结点总是以最短路径被访问,所以第二次路径确定不会比第一次短)
|
||||
|
||||
```cpp
|
||||
#include <queue>
|
||||
|
||||
// 新建一个数据结构,用来描述当前节点状态
|
||||
typedef struct NodeStateStruct {
|
||||
int para1;
|
||||
int para2;
|
||||
int para3;
|
||||
} NodeState;
|
||||
|
||||
int main(void) {
|
||||
// 讨论边界条件,比如字符串长度为 0 之类的
|
||||
|
||||
// 初始化一个队列
|
||||
std::queue<NodeState> queue;
|
||||
// 把根节点放进去
|
||||
queue.push(NodeState {0, 0, 0});
|
||||
// 开始迭代,当队列为空时结束迭代
|
||||
NodeState node;
|
||||
while (!queue.empty()) {
|
||||
// 弹出队首
|
||||
node = queue.front();
|
||||
queue.pop();
|
||||
// 遍历队首的所有子节点并把它们放到队尾
|
||||
queue.push(/* child node 1 */);
|
||||
queue.push(/* child node 2 */);
|
||||
queue.push(/* child node 3 */);
|
||||
}
|
||||
}
|
||||
```
|
||||
69
notes/src/btree_basic.md
Normal file
69
notes/src/btree_basic.md
Normal file
@@ -0,0 +1,69 @@
|
||||
# 理论基础
|
||||
|
||||
## 二叉树的种类
|
||||
|
||||
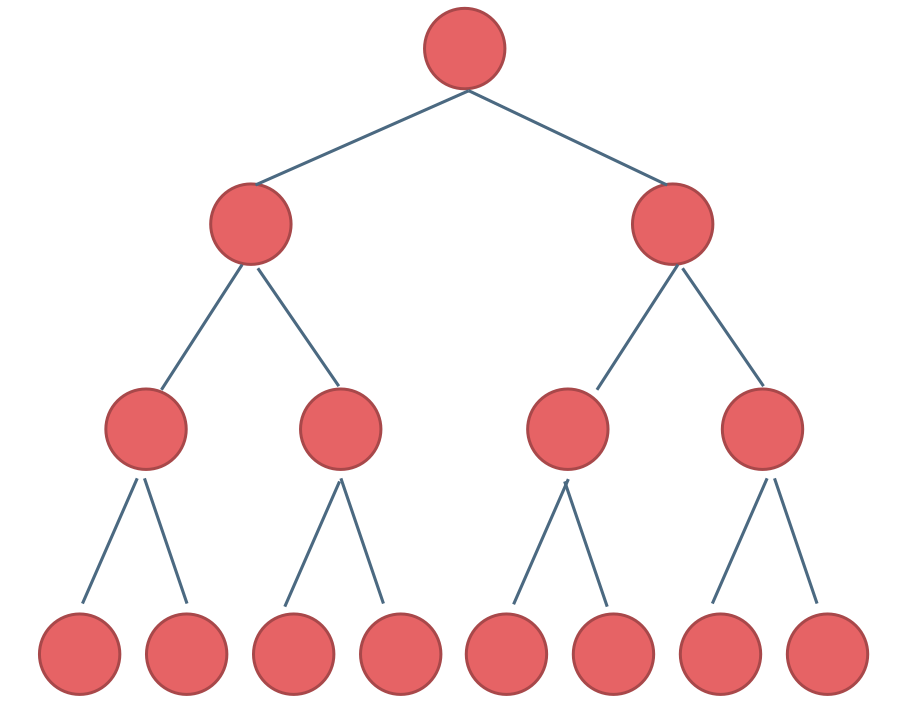
满二叉树:如果一棵二叉树只有度为0的结点和度为2的结点,并且度为0的结点在同一层上,则这棵二叉树为满二叉树。
|
||||
|
||||
|
||||
|
||||
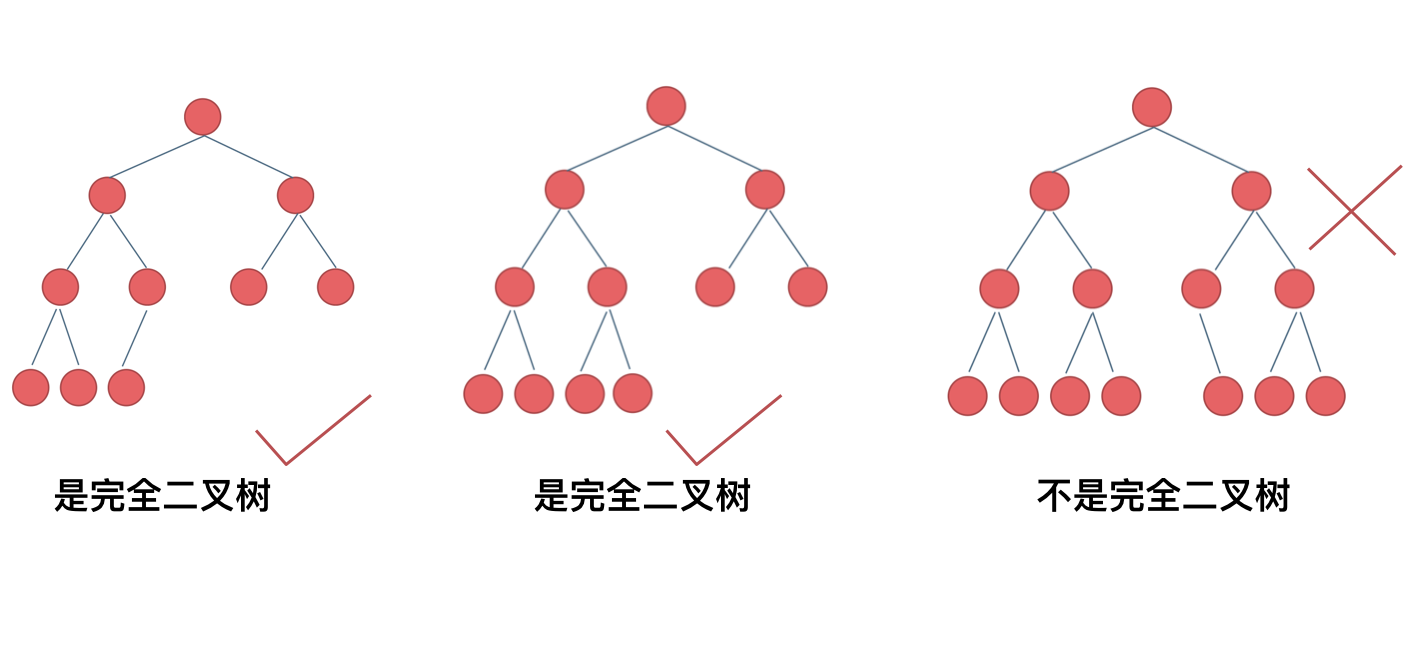
完全二叉树:除了最底层节点可能没填满外,其余每层节点数都达到最大值,并且最下面一层的节点都集中在该层最左边的若干位置。
|
||||
|
||||
|
||||
|
||||
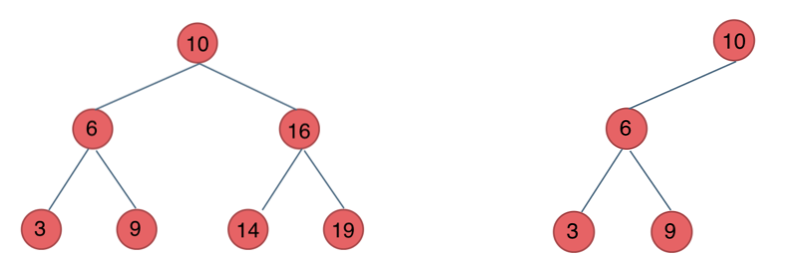
二叉搜索树:
|
||||
|
||||
- 若它的左子树不空,则左子树上所有结点的值均小于它的根结点的值;
|
||||
- 若它的右子树不空,则右子树上所有结点的值均大于它的根结点的值;
|
||||
- 它的左、右子树也分别为二叉排序树。
|
||||
|
||||
|
||||
|
||||
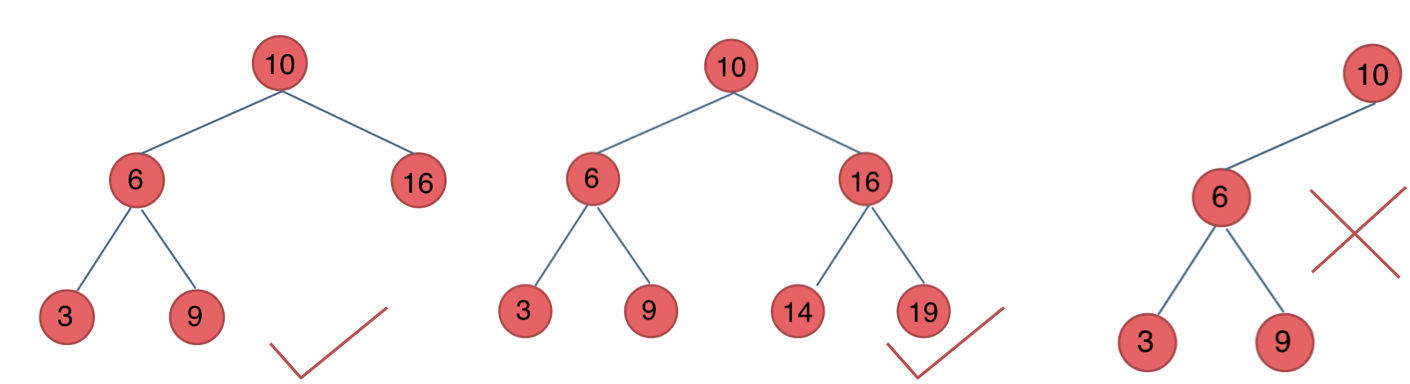
平衡二叉搜索树:又被称为AVL(Adelson-Velsky and Landis)树,且具有以下性质:它是一棵空树或它的左右两个子树的高度差的绝对值不超过1,并且左右两个子树都是一棵平衡二叉树。
|
||||
|
||||
|
||||
|
||||
## 二叉树的存储方式
|
||||
|
||||
1. 链式,用链表来存储
|
||||
|
||||
```cpp
|
||||
struct TreeNode {
|
||||
int val;
|
||||
TreeNode *left;
|
||||
TreeNode *right;
|
||||
TreeNode(int x) : val(x), left(NULL), right(NULL) {}
|
||||
};
|
||||
```
|
||||
|
||||
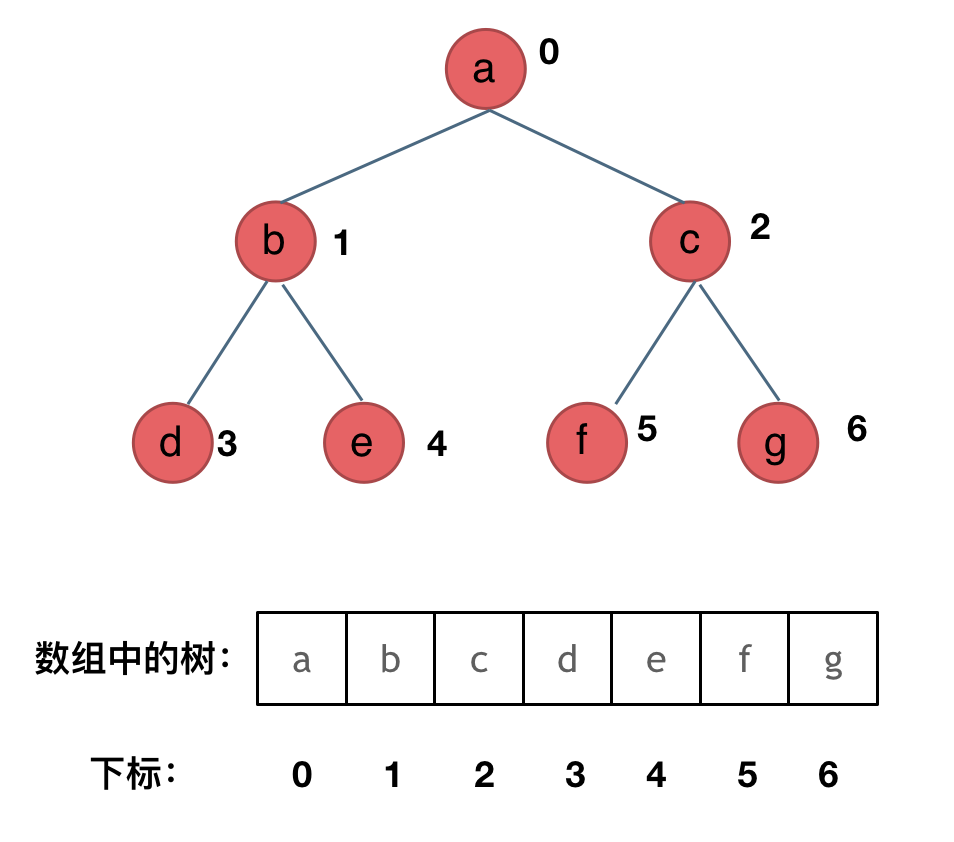
2. 数组存储
|
||||
|
||||
|
||||
|
||||
如果父节点的数组下标是 i,那么它的左孩子就是 i * 2 + 1,右孩子就是 i * 2 + 2。
|
||||
|
||||
## 遍历方式
|
||||
|
||||
- 深度优先遍历
|
||||
- 前序遍历(递归法,迭代法)
|
||||
- 中序遍历(递归法,迭代法)
|
||||
- 后序遍历(递归法,迭代法)
|
||||
- 广度优先遍历
|
||||
- 层序遍历(迭代法)
|
||||
|
||||
深度优先遍历:
|
||||
|
||||
1. 不保留全部节点状态,占用空间小
|
||||
2. 有回溯操作(即有入栈、出栈操作),运行速度慢
|
||||
3. 深度很大的情况下效率不高
|
||||
|
||||
广度优先遍历:
|
||||
|
||||
1. 保留全部节点状态,占用空间大
|
||||
2. 无回溯操作(即无入栈、出栈操作),运行速度快
|
||||
3. 对于解决最短或最少问题特别有效,而且寻找深度小(每个结点只访问一遍,结点总是以最短路径被访问,所以第二次路径确定不会比第一次短)
|
||||
|
||||
区分前中后序遍历的方法:
|
||||
|
||||
- 前序遍历:中左右
|
||||
- 中序遍历:左中右
|
||||
- 后序遍历:左右中
|
||||
159
notes/src/btree_iter.md
Normal file
159
notes/src/btree_iter.md
Normal file
@@ -0,0 +1,159 @@
|
||||
# 遍历
|
||||
|
||||
## 深度优先遍历(递归法)
|
||||
|
||||
```cpp
|
||||
// para_n 用来描述每个节点的状态
|
||||
// 比如 para1 可以是当前节点的指针,para2 和 para3 可以用来表示当前指针的其它状态信息
|
||||
// 遍历结果可以用指针放在接收参数保存,也可以通过声明一个 class 的成员来保存
|
||||
void dfs(int para1, int para2, int para3, std::vector<std::string> &result) {
|
||||
// 讨论边界条件
|
||||
// 只需要在这里讨论结束条件即可,初始化的工作会在 dfs 外完成
|
||||
if (/* end condition */) {
|
||||
/* statement */
|
||||
}
|
||||
// 当当前节点状态越界或不合法时,剪枝
|
||||
if (/* invalid */) {
|
||||
return;
|
||||
}
|
||||
// 当当前节点状态合法时,遍历当前节点的所有子节点
|
||||
dfs(/* state of child node 1 */, result);
|
||||
dfs(/* state of child node 2 */, result);
|
||||
dfs(/* state of child node 3 */, result);
|
||||
}
|
||||
|
||||
void main(void) {
|
||||
dfs(/* state of root node */, /* initial result */);
|
||||
}
|
||||
```
|
||||
|
||||
前中后序遍历的区别就在于访问节点的顺序不同。
|
||||
|
||||
前序遍历:
|
||||
|
||||
```cpp
|
||||
printf("%d\n", curNode->val);
|
||||
dfs(curNode->left, result);
|
||||
dfs(curNode->right, result);
|
||||
```
|
||||
|
||||
中序遍历:
|
||||
|
||||
```cpp
|
||||
dfs(curNode->left, result);
|
||||
printf("%d\n", curNode->val);
|
||||
dfs(curNode->right, result);
|
||||
```
|
||||
|
||||
后序遍历:
|
||||
|
||||
```cpp
|
||||
dfs(curNode->left, result);
|
||||
dfs(curNode->right, result);
|
||||
printf("%d\n", curNode->val);
|
||||
```
|
||||
|
||||
## 深度优先遍历(迭代法)
|
||||
|
||||
由于递归本质是对栈进行操作,因此也可以用迭代+栈的方式实现。
|
||||
|
||||
以中序遍历为例:
|
||||
|
||||
```cpp
|
||||
vector<int> inorderTraversal(TreeNode* root) {
|
||||
// 初始化结果集
|
||||
vector<int> result;
|
||||
// 初始化栈
|
||||
stack<TreeNode*> st;
|
||||
// 当根节点不为空时将根节点入栈
|
||||
if (root != NULL) st.push(root);
|
||||
// 当栈为空时停止迭代
|
||||
while (!st.empty()) {
|
||||
// 先获取栈顶元素
|
||||
TreeNode* node = st.top();
|
||||
// 栈顶元素出栈
|
||||
st.pop();
|
||||
// 如果栈顶元素不为空指针,则将节点按顺序入栈
|
||||
if (node != NULL) {
|
||||
// 注意是右中左,和左中右反着,因为栈是先进后出
|
||||
// 右
|
||||
if (node->right) st.push(node->right);
|
||||
// 中
|
||||
st.push(node);
|
||||
st.push(NULL);
|
||||
// 左
|
||||
if (node->left) st.push(node->left);
|
||||
} else { // 只有遇到空节点的时候,才将下一个节点放进结果集
|
||||
node = st.top(); // 重新取出栈中元素
|
||||
st.pop();
|
||||
result.push_back(node->val); // 加入到结果集
|
||||
}
|
||||
}
|
||||
return result;
|
||||
}
|
||||
```
|
||||
|
||||
## 广度优先遍历(层序遍历)
|
||||
|
||||
```cpp
|
||||
void iter(Node *root) {
|
||||
// 讨论边界条件
|
||||
if (root == nullptr) {
|
||||
return;
|
||||
}
|
||||
// 初始化一个队列
|
||||
std::queue<Node *> queue;
|
||||
// 把根节点放进去
|
||||
if (root) queue.push(root);
|
||||
// 开始迭代,当队列为空时结束迭代
|
||||
while (!queue.empty()) {
|
||||
// 取队首
|
||||
Node *node = queue.front();
|
||||
// 弹出队首
|
||||
queue.pop();
|
||||
// 将队首的值放进向量中
|
||||
vec.push_back(node->val);
|
||||
// 遍历队首的所有子节点并把它们放到队尾
|
||||
if (node->left) queue.push(node->left);
|
||||
if (node->right) queue.push(node->right);
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
如果需要对每一层进行处理,则修改如下:
|
||||
|
||||
```cpp
|
||||
vector<vector<int>> iter(Node *root) {
|
||||
// 讨论边界条件
|
||||
if (root == nullptr) {
|
||||
return;
|
||||
}
|
||||
// 初始化一个队列
|
||||
std::queue<Node *> queue;
|
||||
// 初始化结果向量
|
||||
vector<vector<int>> result;
|
||||
// 把根节点放进去
|
||||
if (root) queue.push(root);
|
||||
// 开始迭代,当队列为空时结束迭代
|
||||
while (!queue.empty()) {
|
||||
// 获得当前层的节点个数
|
||||
int size = queue.size();
|
||||
// 创建一个向量用来装当前层的结果
|
||||
vector<int> vec;
|
||||
// 开始迭代当前层
|
||||
for (int i{0}; i < size; ++i) {
|
||||
// 取队首
|
||||
Node *node = queue.front();
|
||||
// 弹出队首
|
||||
queue.pop();
|
||||
// 将队首的值放进向量中
|
||||
vec.push_back(node->val);
|
||||
// 遍历队首的所有子节点并把它们放到队尾
|
||||
if (node->left) queue.push(node->left);
|
||||
if (node->right) queue.push(node->right);
|
||||
}
|
||||
result.push_back(vec);
|
||||
}
|
||||
return result;
|
||||
}
|
||||
```
|
||||
@@ -1,29 +0,0 @@
|
||||
# 深度优先遍历
|
||||
|
||||
1. 不保留全部节点状态,占用空间小
|
||||
2. 有回溯操作(即有入栈、出栈操作,运行速度慢)
|
||||
3. 深度很大的情况下效率不高
|
||||
|
||||
```cpp
|
||||
// 接收参数用来描述每个节点的状态
|
||||
// 遍历结果可以用指针放在接收参数保存,也可以通过声明一个 class 的成员来保存
|
||||
void dfs(int para1, int para2, int para3, std::vector<std::string> &result) {
|
||||
// 讨论边界条件
|
||||
// 只需要在这里讨论结束条件即可,初始化的工作会在 dfs 外完成
|
||||
if (/* end condition */) {
|
||||
/* statement */
|
||||
}
|
||||
// 当当前节点状态越界或不合法时,剪枝
|
||||
if (/* invalid */) {
|
||||
return;
|
||||
}
|
||||
// 当当前节点状态合法时,遍历当前节点的所有子节点
|
||||
dfs(/* state of child node 1 */, result);
|
||||
dfs(/* state of child node 2 */, result);
|
||||
dfs(/* state of child node 3 */, result);
|
||||
}
|
||||
|
||||
void main(void) {
|
||||
dfs(/* state of root node */, /* initial result */);
|
||||
}
|
||||
```
|
||||
13
notes/src/stl.md
Normal file
13
notes/src/stl.md
Normal file
@@ -0,0 +1,13 @@
|
||||
# 总结
|
||||
|
||||
以下底层实现为二叉搜索树,增删操作时间复杂度是 log(n):
|
||||
|
||||
- `map`
|
||||
- `set`
|
||||
- `multimap`
|
||||
- `multiset`
|
||||
|
||||
以下底层实现是哈希表,增删操作时间复杂度是 log(1):
|
||||
|
||||
- `unordered_map`
|
||||
- `unordered_set`
|
||||
Reference in New Issue
Block a user